
【题目】已知椭圆![]() ,四点
,四点![]() ,
,![]() ,
, ,
, ,恰有三点在椭圆
,恰有三点在椭圆![]() 上.
上.
(1)求![]() 的方程;
的方程;
(2)设![]() 、
、![]() 为椭圆
为椭圆![]() 在左、右焦点,
在左、右焦点,![]() 是椭圆在第一象限上一点,满足
是椭圆在第一象限上一点,满足![]() ,求
,求![]() 面积的最大值.
面积的最大值.
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:高中数学 来源: 题型:
【题目】某制药厂准备投入适当的广告费,对产品进行宣传,在一年内,预计年销量Q(万件)与广告费x(万元)之间的函数关系为Q![]() (x≥0).已知生产此产品的年固定投入为3万元,每生产1万件此产品仍需后期再投入32万元,若每件售价为“年平均每件投入的150%”与“年平均每件所占广告费的50%”之和(注:投入包括“年固定投入”与“后期再投入”).
(x≥0).已知生产此产品的年固定投入为3万元,每生产1万件此产品仍需后期再投入32万元,若每件售价为“年平均每件投入的150%”与“年平均每件所占广告费的50%”之和(注:投入包括“年固定投入”与“后期再投入”).
(1)试将年利润w万元表示为年广告费x万元的函数,并判断当年广告费投入100万元时,企业亏损还是盈利?
(2)当年广告费投入多少万元时,企业年利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出如下四个命题:①若“![]() 且
且![]() ”为假命题,则
”为假命题,则![]() 均为假命题;②命题“若
均为假命题;②命题“若![]() ,则
,则![]() ”的否命题为“若
”的否命题为“若![]() ,则
,则![]() ”;③命题“
”;③命题“![]() ,
,![]() ”的否定是“
”的否定是“![]() ,
,![]() ”;④在
”;④在![]() 中,“
中,“![]() ”是“
”是“![]() ”的充要条件.其中正确的命题是( )
”的充要条件.其中正确的命题是( )
A.②③④B.①③④C.①②④D.①②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若![]() ,
,![]() ,求
,求![]() 的值域;
的值域;
(2)当![]() 时,求
时,求![]() 的最小值
的最小值![]() ;
;
(3)是否存在实数![]() 、
、![]() ,同时满足下列条件:①
,同时满足下列条件:① ![]() ;② 当
;② 当![]() 的定义域为
的定义域为![]() 时,其值域为
时,其值域为![]() .若存在,求出
.若存在,求出![]() 、
、![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某动物园要为刚入园的小动物建造一间两面靠墙的三角形露天活动室,地面形状如图所示,已知已有两面墙的夹角为![]() ,墙
,墙![]() 的长度为
的长度为![]() 米,(已有两面墙的可利用长度足够大),记
米,(已有两面墙的可利用长度足够大),记![]() .
.
(1)若![]() ,求
,求![]() 的周长(结果精确到0.01米);
的周长(结果精确到0.01米);
(2)为了使小动物能健康成长,要求所建的三角形露天活动室面积,![]() 的面积尽可能大,当
的面积尽可能大,当![]() 为何值时,该活动室面积最大?并求出最大面积.
为何值时,该活动室面积最大?并求出最大面积.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]()
![]() 平面
平面![]() ,△
,△![]() 为等边三角形,
为等边三角形,![]() ,
,![]() ,
,![]() ,
,![]() 分别为棱
分别为棱![]() ,
,![]() 的中点.
的中点.
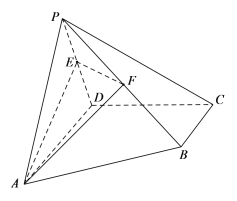
(1)求证:![]() 平面
平面![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值;
所成锐二面角的余弦值;
(3)在棱![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求
?若存在,求![]() 的值,若不存在,说明理由.
的值,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年国庆黄金周影市火爆依旧,《我和我的祖国》、《中国机长》、《攀登者》票房不断刷新,为了解我校高三2300名学生的观影情况,随机调查了100名在校学生,其中看过《我和我的祖国》或《中国机长》的学生共有80位,看过《中国机长》的学生共有60位,看过《中国机长》且看过《我和我的祖国》的学生共有50位,则该校高三年级看过《我和我的祖国》的学生人数的估计值为( )
A.1150B.1380C.1610D.1860
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数![]() ,若在定义域内存在实数
,若在定义域内存在实数![]() ,满足
,满足![]() ,则称
,则称![]() 为“
为“![]() 类函数”.
类函数”.
(1)已知函数![]() ,试判断
,试判断![]() 是否为“
是否为“![]() 类函数”?并说明理由;
类函数”?并说明理由;
(2)设![]() 是定义在
是定义在![]() 上的“
上的“![]() 类函数”,求是实数
类函数”,求是实数![]() 的最小值;
的最小值;
(3)若
![]() 为其定义域上的“
为其定义域上的“![]() 类函数”,求实数
类函数”,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com