
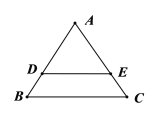
【题目】已知边长为4的正三角形ABC的边AB、AC上分别有两点D、E,DE//BC且DE=3,现将△ABC沿DE折成直二面角A﹣DE﹣B,在空间中取一点F使得ADBF为平行四边形,连接AC、FC得六面体ABCEDF,G是BC边上动点.
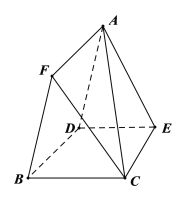
(1)若EG//平面ACF,求CG的长;
(2)若G为BC中点,求二面角G﹣AE﹣D的平面角的余弦值.
【答案】(1)1;(2)![]() .
.
【解析】
(1)由平行四边形可得AF//BD,则BD//平面ACF,再由平面ACF∩平面BCED=CH,可得BD//CH,同理EG//CH,则BD//EG,即可求解;
(2)取DE中点O,连接AO,OG(取BC中点G),以O为坐标原点,分别以OG,OE,OA所在直线为x,y,z轴建立空间直角坐标系,求得平面AEG的法向量,取平面AED的一个法向量为![]() ,进而利用数量积求解即可.
,进而利用数量积求解即可.
(1)设平面ACF与平面BCED的交线为CH(H在直线DE上),
∵ADBF为平行四边形,∴AF//BD,
∵AF平面ACF,BD平面ACF,
∴BD//平面ACF,
又BD平面BCED, 平面ACF∩平面BCED=CH,∴BD//CH,
∵EG//平面ACF,EG平面BCED,平面ACF∩平面BCED=CH,∴EG//CH,
∴BD//EG,
∴![]() 是平行四边形,
是平行四边形,
∴BG=DE=3,则CG=BC-BG=1
(2)取DE中点O,连接AO,OG(取BC中点G),则AO⊥DE,OG⊥DE,
又平面ADE⊥平面BCED,且平面ADE∩BCED=DE,∴AO⊥平面BCED,
以O为坐标原点,分别以OG,OE,OA所在直线为x,y,z轴建立空间直角坐标系,如图所示,
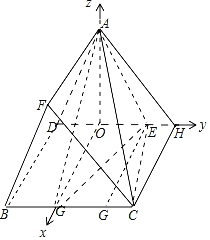
则E(0,![]() ,0),A(0,0,
,0),A(0,0,![]() ),G(
),G(![]() ,0,0),
,0,0),
则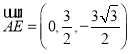 ,
,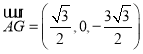 ,
,
设平面AEG的法向量为![]() ,
,
由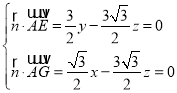 ,取z=1,得
,取z=1,得![]() ,
,
取平面AED的一个法向量为![]() ,
,
∴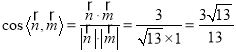 ,
,
∴二面角G﹣AE﹣D的平面角的余弦值为![]() .
.


科目:高中数学 来源: 题型:
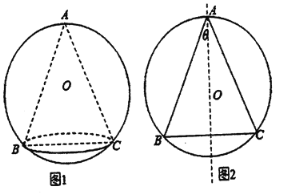
【题目】某艺术品公司欲生产一款迎新春工艺礼品,该礼品是由玻璃球面和该球的内接圆锥组成,圆锥的侧面用于艺术装饰,如图1.为了便于设计,可将该礼品看成是由圆O及其内接等腰三角形![]() 绕底边
绕底边![]() 上的高所在直线
上的高所在直线![]() 旋转
旋转![]() 而成,如图2.已知圆O的半径为
而成,如图2.已知圆O的半径为![]() ,设
,设![]() ,
,![]() ,圆锥的侧面积为
,圆锥的侧面积为![]() (S圆锥的侧面积
(S圆锥的侧面积![]() (R-底面圆半径,I-母线长))
(R-底面圆半径,I-母线长))
(1)求S关于![]() 的函数关系式;
的函数关系式;
(2)为了达到最佳观赏效果,要求圆锥的侧面积S最大.求S取得最大值时腰![]() 的长度
的长度
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代的数学名著,书中有如下问题:“今有五人分五钱,令上两人所得与下三人等。问各得几何?”其意思是:“已知甲、乙、丙、丁、戊五人分五钱,甲、乙两人所得之和与丙、丁、戊三人所得之和相等,且甲、乙、丙、丁、戊所得依次成等差数列。问五人各得多少钱?”(“钱”是古代的一种重量单位)。这个问题中,戊所得为( )
A. ![]() 钱 B.
钱 B. ![]() 钱 C.
钱 C. ![]() 钱 D.
钱 D. ![]() 钱
钱
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设a为常数,函数f(x)=x(lnx﹣1)﹣ax2,给出以下结论:(1)f(x)存在唯一零点与a的取值无关;(2)若a=e﹣2,则f(x)存在唯一零点;(3)若a<e﹣2,则f(x)存在两个零点.其中正确的个数是( )
A.3B.2C.1D.0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点是
的左、右焦点是![]() ,左右顶点是
,左右顶点是![]() ,离心率是
,离心率是![]() ,过
,过![]() 的直线与椭圆交于两点P、Q(不是左、右顶点),且
的直线与椭圆交于两点P、Q(不是左、右顶点),且![]() 的周长是
的周长是![]() ,
,
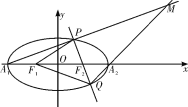
直线![]() 与
与![]() 交于点M.
交于点M.
(1)求椭圆的方程;
(2)(ⅰ)求证直线![]() 与
与![]() 交点M在一条定直线l上;
交点M在一条定直线l上;
(ⅱ)N是定直线l上的一点,且PN平行于x轴,证明:![]() 是定值.
是定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体![]() 中,点
中,点![]() 是棱
是棱![]() 上的一个动点,平面
上的一个动点,平面![]() 交棱
交棱![]() 于点
于点![]() .下列命题正确的为_______________.
.下列命题正确的为_______________.
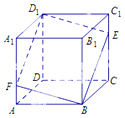
①存在点![]() ,使得
,使得![]() //平面
//平面![]() ;
;
②对于任意的点![]() ,平面
,平面![]() 平面
平面![]() ;
;
③存在点![]() ,使得
,使得![]() 平面
平面![]() ;
;
④对于任意的点![]() ,四棱锥
,四棱锥![]() 的体积均不变.
的体积均不变.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列1,2,1,2,2,1,2,2,2,1,2,2,2,2,1,2,![]() ,其相邻的两个1被2隔开,第
,其相邻的两个1被2隔开,第![]() 对1之间有
对1之间有![]() 个2,则数列的前209项的和为( )
个2,则数列的前209项的和为( )
A. 279 B. 289 C. 399 D. 409
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C:x2+y2+2kx+(4k+10)y+10k+20=0,其中k≠-1.
(1)求证:曲线C都表示圆,并且这些圆心都在同一条直线上;
(2)证明:曲线C过定点;
(3)若曲线C与x轴相切,求k的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com