
如图,已知直平行六面体ABCD-A1B1C1D1中,AD⊥BD,AD=BD=a,E是CC1的中点,A![]() D⊥BE.
D⊥BE.
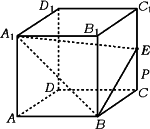
(1)求证:A1D⊥平面BDE;
(2)求二面角B-DE-C的大小;
(3)求点B到平面A1DE的距离.
|
解:(1)∵直平行六面体ABCD-A1B1C1D1中,AA1⊥面ABCD, 又∵AD⊥BD,∴A1D⊥BD,又A1D⊥BE,∴A1D⊥平面BDE. (2)连B1C,∵A1B1平行且等于CD,∴B1C平行且等于A1D. ∵A1D⊥BE,∴B1C⊥BE,∴∠BB1C=∠CBE, ∴Rt△BB1C∽Rt△CBE,∴ ∵CE= ∴ 取CD中点M,连BM,∵CD= 过M作MN⊥DE于N,连BN. ∵平面CD1⊥平面BD,BM⊥CD,∴BM⊥平面CD1,∴BN⊥DE1, ∴∠BNM就是二面角B-DE-C的平面角, ∵sin∠MDN= ∴MN= 在Rt△BMN中,tan∠BNM= 即二面角B-DE-C等于arctan (3)∵A1D⊥平面BDE,BN ∴BN⊥平面A1DE,即BN的长就是点B到平面A1DE的距离. ∵BM= 即点B到平面A1DE的距离为 |


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源: 题型:
 如图,已知直平行六面体ABCD-A1B1C1D1中,AD⊥BD,AD=BD=a,E是CC1的中点,A1D⊥BE.
如图,已知直平行六面体ABCD-A1B1C1D1中,AD⊥BD,AD=BD=a,E是CC1的中点,A1D⊥BE.查看答案和解析>>
科目:高中数学 来源: 题型:
(本题满分12分)如图,已知直平行六面体ABCD—A![]() B
B![]() C
C![]() D
D![]() 中,AD⊥BD,AD=BD=a,E是CC
中,AD⊥BD,AD=BD=a,E是CC![]() 的中点,A1D⊥BE.
的中点,A1D⊥BE.
(1)求证:A![]() D⊥平面BDE;(2)求二面角B—DE—C的大小;(3)求点B到平面A
D⊥平面BDE;(2)求二面角B—DE—C的大小;(3)求点B到平面A![]() DE的距离.
DE的距离.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年吉林省高三上学期阶段验收数学试卷(解析版) 题型:解答题
(本题满分12分)
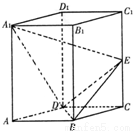
如图,已知直平行六面体ABCD-A1B1C1D1中,AD⊥BD,AD=BD=a,E是CC1的中点,A1D⊥BE.

(I)求证:A1D⊥平面BDE;
(II)求二面角B―DE―C的大小;
(III)求点B到平面A1DE的距离
查看答案和解析>>
科目:高中数学 来源:2004年江苏省无锡市高三调研数学试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com