
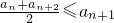 且an≤M(M是与n无关的常数)的无穷数列an称为T数列.
且an≤M(M是与n无关的常数)的无穷数列an称为T数列.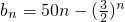 ,且数列bn是T数列,求常数M的取值范围;
,且数列bn是T数列,求常数M的取值范围;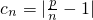 (n∈N*,p>1),问数列bn是否是T数列?请说明理由.
(n∈N*,p>1),问数列bn是否是T数列?请说明理由.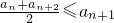 .(2分)
.(2分)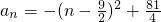 ,当n=4或5时,an取得最大值20,即an≤20.
,当n=4或5时,an取得最大值20,即an≤20.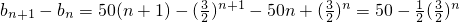 ,
,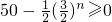 即n≤11时,bn+1-bn>0,此时数列bn单调递增(6分)
即n≤11时,bn+1-bn>0,此时数列bn单调递增(6分)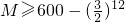 (9分)
(9分)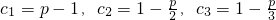 ,
, 得
得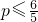 ,
, 时符合
时符合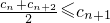 条件.(11分)
条件.(11分) ,此时
,此时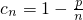
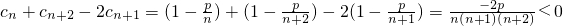
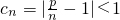 ,
, 时数列cn是T数列;(13分)
时数列cn是T数列;(13分)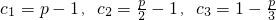 ,
, ,所以2<p≤3时数列cn不是T数列.(15分)
,所以2<p≤3时数列cn不是T数列.(15分)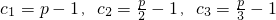 ,
,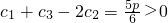 ,所以p>3时数列cn不是T数列.(17分)
,所以p>3时数列cn不是T数列.(17分) 时数列cn是T数列;当
时数列cn是T数列;当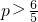 时数列cn不是T数列.(18分)
时数列cn不是T数列.(18分)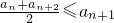 .由此能够证明数列an是T数列.
.由此能够证明数列an是T数列.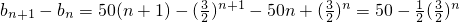 ,所以当
,所以当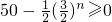 即n≤11时,bn+1-bn>0,此时数列bn单调递增.当n≥12时,bn+1-bn<0,此时数列bn单调递减;故数列bn的最大项是b12,由此能求出M的取值范围.
即n≤11时,bn+1-bn>0,此时数列bn单调递增.当n≥12时,bn+1-bn<0,此时数列bn单调递减;故数列bn的最大项是b12,由此能求出M的取值范围.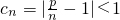 ,所以当
,所以当 时数列cn是T数列;当2<p≤3时,数列cn不是T数列.当p>3时,数列cn不是T数列.
时数列cn是T数列;当2<p≤3时,数列cn不是T数列.当p>3时,数列cn不是T数列.

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2012年北京市怀柔区高考数学二模试卷(理科)(解析版) 题型:解答题
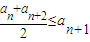 且an≤M(M是与n无关的常数)的无穷数列an称为T数列.
且an≤M(M是与n无关的常数)的无穷数列an称为T数列.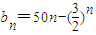 ,且数列bn是T数列,求常数M的取值范围;
,且数列bn是T数列,求常数M的取值范围; (n∈N*,p>1),问数列bn是否是T数列?请说明理由.
(n∈N*,p>1),问数列bn是否是T数列?请说明理由.查看答案和解析>>
科目:高中数学 来源:2011年江苏省高考数学权威预测试卷(1)(解析版) 题型:解答题
 且an≤M(M是与n无关的常数)的无穷数列an称为T数列.
且an≤M(M是与n无关的常数)的无穷数列an称为T数列. ,且数列bn是T数列,求常数M的取值范围;
,且数列bn是T数列,求常数M的取值范围; (n∈N*,p>1),问数列bn是否是T数列?请说明理由.
(n∈N*,p>1),问数列bn是否是T数列?请说明理由.查看答案和解析>>
科目:高中数学 来源:2011年上海市闵行区高考数学三模试卷(文理合卷)(解析版) 题型:解答题
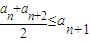 且an≤M(M是与n无关的常数)的无穷数列an称为T数列.
且an≤M(M是与n无关的常数)的无穷数列an称为T数列.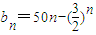 ,且数列bn是T数列,求常数M的取值范围;
,且数列bn是T数列,求常数M的取值范围;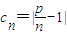 (n∈N*,p>1),问数列bn是否是T数列?请说明理由.
(n∈N*,p>1),问数列bn是否是T数列?请说明理由.查看答案和解析>>
科目:高中数学 来源:2011年上海市闵行区高考数学二模试卷(理科)(解析版) 题型:解答题
 且an≤M(M是与n无关的常数)的无穷数列an称为T数列.
且an≤M(M是与n无关的常数)的无穷数列an称为T数列.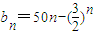 ,且数列bn是T数列,求常数M的取值范围;
,且数列bn是T数列,求常数M的取值范围; (n∈N*,p>1),问数列bn是否是T数列?请说明理由.
(n∈N*,p>1),问数列bn是否是T数列?请说明理由.查看答案和解析>>
科目:高中数学 来源:2011年上海市闵行区高考数学二模试卷(文科)(解析版) 题型:解答题
 且an≤M(M是与n无关的常数)的无穷数列an称为T数列.
且an≤M(M是与n无关的常数)的无穷数列an称为T数列. ,且数列bn是T数列,求常数M的取值范围;
,且数列bn是T数列,求常数M的取值范围; (n∈N*,p>1),问数列bn是否是T数列?请说明理由.
(n∈N*,p>1),问数列bn是否是T数列?请说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com