
【题目】已知函数![]() .
.
(1)若![]() ,试判断函数
,试判断函数![]() 的零点个数;
的零点个数;
(2)若函数![]() 在
在![]() 上为增函数,求整数
上为增函数,求整数![]() 的最大值,(可能要用的数据:
的最大值,(可能要用的数据: ![]() ;
; ![]() ).
).
【答案】(1)1个;(2)6
【解析】试题分析:(Ⅰ)根据导数求解函数![]() 的单调性,利用零点的存在定理,即可判定函数
的单调性,利用零点的存在定理,即可判定函数![]() 在
在![]() 上的零点的个数.
上的零点的个数.
(Ⅱ)由题意,把![]() 在
在![]() 上恒成立,
上恒成立, ![]() 在
在![]() 上恒成立,进而转化为
上恒成立,进而转化为
![]() 在
在![]() 上恒成立,令
上恒成立,令![]() ,即
,即![]() ,利用导数求解函数
,利用导数求解函数![]() 的单调性和最小值,即可求解实数
的单调性和最小值,即可求解实数![]() 的取值范围.
的取值范围.
试题解析:
(1)因为![]() ,易知
,易知![]() 在
在![]() 上为增函数,则
上为增函数,则![]() ,
,
故![]() 在
在![]() 上为增函数,又
上为增函数,又![]() ,
, ![]() ,
,
所以函数![]() 在
在![]() 上的零点有且只有1个.
上的零点有且只有1个.
(2)因为![]() ,由题意
,由题意![]() 在
在![]() 上恒成立,
上恒成立,
因为![]() 显然成立,故只需
显然成立,故只需![]() 在
在![]() 上恒成立,
上恒成立,
令![]() ,则
,则![]()
因为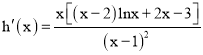
由(1)可知: ![]() 在
在![]() 上为增函数,故
上为增函数,故![]() 在
在![]() 上有唯一零点记为
上有唯一零点记为![]() ,
, ![]()
![]() ,
, ![]()
![]() ,
,
则![]() ,
, ![]()
![]() ,
,
则![]() 在
在![]() 为减函数,
为减函数,
![]() 在
在![]() 为增函数,
为增函数,
故![]() 时,
时, ![]() 有最小值
有最小值![]() .
.
令![]() ,则
,则![]() 最小值有
最小值有![]()
![]() ,
,
因![]() ,则
,则![]() 的最小值大约在
的最小值大约在![]() 之间,故整数
之间,故整数![]() 的最大值为6.
的最大值为6.


 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:高中数学 来源: 题型:
【题目】已知方程C:x2+y2﹣2x﹣4y+m=0,
(1)若方程C表示圆,求实数m的范围;
(2)在方程表示圆时,该圆与直线l:x+2y﹣4=0相交于M、N两点, ![]() ,求m的值;
,求m的值;
(3)在(2)的条件下,定点A(1,0),P在线段MN上运动,求直线AP的斜率取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】供电部门对某社区![]() 位居民2016年11月份人均用电情况进行统计后,按人均用电量分为
位居民2016年11月份人均用电情况进行统计后,按人均用电量分为![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 五组,整理得到如下的频率分布直方图,则下列说法错误的是( )
五组,整理得到如下的频率分布直方图,则下列说法错误的是( )
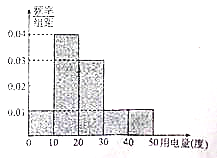
A. 11月份人均用电量人数最多的一组有![]() 人
人
B. 11月份人均用电量不低于![]() 度的有
度的有![]() 人
人
C. 11月份人均用电量为![]() 度
度
D. 在这![]() 位居民中任选
位居民中任选![]() 位协助收费,选到的居民用电量在
位协助收费,选到的居民用电量在![]() 一组的概率为
一组的概率为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据下列条件,求直线的方程:
(Ⅰ)过直线l1:2x﹣3y﹣1=0和l2:x+y+2=0的交点,且垂直于直线2x﹣y+7=0;
(Ⅱ)过点(﹣3,1),且在两坐标轴上的截距之和为﹣4.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产甲、乙两种产品,已知生产每吨甲、乙两种产品所需煤、电力、劳动力、获得利润及每天资源限额(量大供应量)如下表所示:
资源\消耗量\产品 | 甲产品(每吨) | 乙产品(每吨) | 资源限额(每天) |
煤(t) | 9 | 4 | 360 |
电力(kwh) | 4 | 5 | 200 |
劳动力(个) | 3 | 10 | 300 |
利润(万元) | 6 | 12 |
问:每天生产甲、乙两种产品各多少吨,获得利润总额最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知方程x2+y2﹣2(m+3)x+2(1﹣4m2)y+16m4+9=0表示一个圆.
(1)求实数m的取值范围;
(2)求该圆半径r的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,AC=3,BC=4,AA1=4,AB=5,点D是AB的中点. 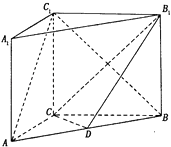
(1)求证:AC⊥BC1;
(2)求证:AC1∥平面CDB1 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com