
| A�� | f��x����ͼ�����ֱ��x=$\frac{��}{3}$�Գƣ�g��x��ͼ�����ԭ��Գ� | |
| B�� | f��x����ͼ����ڵ㣨$\frac{��}{4}$��0���Գƣ�g��x��ͼ�����ֱ��x=$\frac{��}{4}$�Գ� | |
| C�� | f��x����ͼ�����ֱ��x=$\frac{��}{6}$�Գƣ�g��x��ͼ�����ԭ��Գ� | |
| D�� | f��x����ͼ����ڵ㣨$\frac{5��}{12}$��0���Գƣ�g��x��ͼ�����ֱ��x=$\frac{��}{6}$�Գ� |
���� �������������Ǻ�ȱ任������f��x���Ľ���ʽ������y=Asin����x+�գ���ͼ��任�������g��x���Ľ���ʽ�����������Һ�������ֵ�Լ�����ͼ��ĶԳ��ԣ��ó����ۣ�
��� �⣺�ߺ���f��x��=$\sqrt{3}$asin��xcos��x+acos2��x-$\frac{1}{2}$=$\frac{\sqrt{3}}{2}$asin��x+$\frac{a}{2}$cos��x+$\frac{a-1}{2}$
=asin����x+$\frac{��}{6}$��+$\frac{a-1}{2}$��
�ɺ��������ֵΪa+$\frac{a-1}{2}$=1���ɵ� a=1��
�ٸ��ݺ�����ͼ�����������Գ���ľ���Ϊ$\frac{T}{2}$=$\frac{��}{��}$=$\frac{��}{2}$����æ�=2��
�� f��x��=sin��2x+$\frac{��}{6}$����
��������f��x����ͼ������ƽ��$\frac{��}{12}$����λ������ͼ���Ӧ����Ϊg��x��=sin[2��x-$\frac{��}{12}$��+$\frac{��}{6}$]=sin2x��
��x=$\frac{��}{3}$ʱ��f��x��=$\frac{1}{2}$��������ֵ����f��x����ͼ����ֱ��x=$\frac{��}{3}$�Գƣ����ų�A��
��x=$\frac{��}{4}$ʱ��f��x��=$\frac{\sqrt{3}}{2}$����f��x����ͼ���ڵ㣨$\frac{��}{4}$��0���Գƣ����ų�B��
��x=$\frac{��}{6}$ʱ��f��x��=1���Ǻ��������ֵ����f��x����ͼ�����ֱ��x=$\frac{��}{6}$�Գƣ�g��x��ͼ�����ԭ��Գƣ�
��C����������
��x=$\frac{5��}{12}$ʱ��f��x��=0���Ǻ��������ֵ����f��x����ͼ����ڣ�$\frac{5��}{12}$��0���Գƣ�������g��x��=sin2x��
ͼ����ֱ��x=$\frac{��}{6}$�Գƣ����ų�D��
��ѡ��C��
���� ������Ҫ�������Ǻ�ȱ任��������y=Asin����x+�գ���ͼ��任���ɣ����Һ�������ֵ�Լ�����ͼ��ĶԳ��ԣ������е��⣮


 һŵ��ҵ�����ҵ���ּ�����������������ϵ�д�
һŵ��ҵ�����ҵ���ּ�����������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{7}{5}$ | B�� | 2 | C�� | $\frac{9}{5}$ | D�� | $\frac{11}{5}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
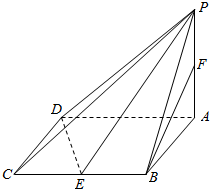 ������P-ABCD�У�����ABCD�DZ߳�Ϊ2�����Σ���BAD=60�㣬PA����ABCD��PA=$\sqrt{3}$��E��F�ֱ�ΪBC��PA���е㣮
������P-ABCD�У�����ABCD�DZ߳�Ϊ2�����Σ���BAD=60�㣬PA����ABCD��PA=$\sqrt{3}$��E��F�ֱ�ΪBC��PA���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-�ޣ�-3���ȣ�0��3�� | B�� | ��-3��0���ȣ�3��+�ޣ� | C�� | ��-�ޣ�-3���ȣ�3��+�ޣ� | D�� | ��-3��0���ȣ�0��3�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com