
【题目】已知函数f(x)=x|x﹣a|,a∈R,g(x)=x2﹣1.
(1)当a=1时,解不等式f(x)≥g(x);
(2)记函数f(x)在区间[0,2]上的最大值为F(a),求F(a)的表达式.
【答案】
(1)解:f(x)≥g(x),a=1时,即解不等式x|x﹣1|≥x2﹣1,
当x≥1时,不等式为x2﹣x≥x2﹣1,解得x≤1,所以x=1;
当x<1时,不等式为x﹣x2≥x2﹣1,解得 ![]() ,
,
所以 ![]() ;
;
综上,x∈ ![]() .
.
(2)解:因为x∈[0,2],当a≤0时,f(x)=x2﹣ax,则f(x)在区间[0,2]上是增函数,
所以F(a)=f(2)=4﹣2a;
当0<a<2时, ![]() ,
,
则f(x)在区间 ![]() 上是增函数,在区间
上是增函数,在区间 ![]() 上是减函数,在区间[a,2]上是增函数,
上是减函数,在区间[a,2]上是增函数,
所以F(a)=max{f( ![]() ),f(2)},
),f(2)},
而 ![]() ,f(2)=4﹣2a,令
,f(2)=4﹣2a,令 ![]() 即
即 ![]() ,
,
解得 ![]() ,
,
所以当 ![]() 时,F(a)=4﹣2a;
时,F(a)=4﹣2a;
令 ![]() 即
即 ![]() ,解得
,解得 ![]() 或
或 ![]() ,
,
所以当 ![]() 时,
时, ![]() ;
;
当a≥2时,f(x)=﹣x2+ax,
当 ![]() 即2≤a<4时,f(x)在间
即2≤a<4时,f(x)在间 ![]() 上是增函数,在
上是增函数,在 ![]() 上是减函数,
上是减函数,
则 ![]() ;
;
当 ![]() ,即a≥4时,f(x)在间[0,2]上是增函数,则F(a)=f(2)=2a﹣4;
,即a≥4时,f(x)在间[0,2]上是增函数,则F(a)=f(2)=2a﹣4;
所以, 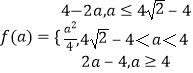
【解析】(1)当a=1时,即解不等式x|x﹣1|≥x2﹣1|,分类讨论,分别解关于x的不等式,最后取两部分的并集即可得到原不等式的解集;(2)由题意,分类讨论,确定函数的单调性,可得F(a)的表达式.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣kx+(2k﹣3).
(1)若k= ![]() 时,解不等式f(x)>0;
时,解不等式f(x)>0;
(2)若f(x)>0对任意x∈R恒成立,求实数k的取值范围;
(3)若函数f(x)两个不同的零点均大于 ![]() ,求实数k的取值范围.
,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2017广东佛山二模】已知椭圆![]() :
: ![]() (
(![]() )的焦距为4,左、右焦点分别为
)的焦距为4,左、右焦点分别为![]() 、
、![]() ,且
,且![]() 与抛物线
与抛物线![]() :
: ![]() 的交点所在的直线经过
的交点所在的直线经过![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)过![]() 的直线
的直线![]() 与
与![]() 交于
交于![]() ,
, ![]() 两点,与抛物线
两点,与抛物线![]() 无公共点,求
无公共点,求![]() 的面积的取值范围.
的面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,△ABC的顶点都在圆O上,点P在BC的延长线上,且PA与圆O切于点A. 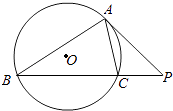
(1)若∠ACB=70°,求∠BAP的度数;
(2)若 ![]() =
= ![]() ,求
,求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣3|﹣|x﹣a|.
(1)当a=2时,解不等式f(x)≤﹣ ![]() ;
;
(2)若存在实数x,使得不等式f(x)≥a成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 且Sn= ![]() +
+ ![]() .
.
(1)求数列{an}的通项公式;
(2)若数列{bn}满足bn=an+2﹣an+ ![]() ,且数列{bn}的前n项和为Tn , 求证:Tn<2n+
,且数列{bn}的前n项和为Tn , 求证:Tn<2n+ ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an},{bn},Sn为数列{an}的前n项和,向量 ![]() =(1,bn),
=(1,bn), ![]() =(an﹣1,Sn),
=(an﹣1,Sn), ![]() ∥
∥ ![]() .
.
(1)若bn=2,求数列{an}通项公式;
(2)若bn= ![]() ,a2=0.
,a2=0.
①证明:数列{an}为等差数列;
②设数列{cn}满足cn= ![]() ,问是否存在正整数l,m(l<m,且l≠2,m≠2),使得cl、c2、cm成等比数列,若存在,求出l、m的值;若不存在,请说明理由.
,问是否存在正整数l,m(l<m,且l≠2,m≠2),使得cl、c2、cm成等比数列,若存在,求出l、m的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市100户居民的月平均用电量(单位:度),以[160,180),[180,200),[200,220),[220.240),[240,260),[260,280),[280,300)分组的频率分布直方图如图. 
(1)求直方图中x的值;
(2)求月平均用电量的众数和中位数;
(3)在月平均用电量为,[220,240),[240,260),[260,280),[280,300)的四组用户中,用分层抽样的方法抽取11户居民,则月平均用电量在[220,240)的用户中应抽取多少户?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对任意m∈R,直线mx﹣y+1=0与圆x2+y2=r2(r>0)交于不同的两点A、B,且存在m使| ![]() +
+ ![]() |≥|
|≥| ![]() |(O是坐标原点)成立,那么r的取值范围是( )
|(O是坐标原点)成立,那么r的取值范围是( )
A.0<r≤ ![]()
B.1<r< ![]()
C.1<r≤ ![]()
D.r> ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com