
分析 (Ⅰ)利用抛物线的定义直接求抛物线C的方程;
(Ⅱ)过焦点F作两条相互垂直的直线,设MN:x=my+$\frac{1}{4}$,PQ:x=-$\frac{1}{m}$y+$\frac{1}{4}$(m≠0),联立直线与抛物线方程组成方程组,利用弦长公式,求出MN,PQ,推出四边形MPNQ的面积的表达式,利用基本不等式求四边形MPNQ面积的最小值.
解答 解:(Ⅰ)由已知:1+$\frac{p}{2}$=$\frac{5}{4}$,∴p=$\frac{1}{2}$
故抛物线C的方程为:y2=x…(4分)
(Ⅱ)由(Ⅰ)知:F($\frac{1}{4}$,0)
设MN:x=my+$\frac{1}{4}$,PQ:x=-$\frac{1}{m}$y+$\frac{1}{4}$(m≠0)…(6分)
由$\left\{\begin{array}{l}{x=my+\frac{1}{4}}\\{{y}^{2}=x}\end{array}\right.$得:y2-my-$\frac{1}{4}$=0
∵△=m2+1>0
∴|MN|=$\sqrt{1+{m}^{2}}•\sqrt{{m}^{2}+1}$=m2+1…(8分)
同理:|PQ|=$\frac{1}{{m}^{2}}$+1…(10分).
∴四边形MPNQ的面积:S=$\frac{1}{2}$(m2+1)($\frac{1}{{m}^{2}}$+1)=$\frac{1}{2}$(2+$\frac{1}{{m}^{2}}$+m2)≥2
(当且仅当m=±1时等号成立)
∴四边形MPNQ的面积的最小值为2.…(12分)
点评 本题考查抛物线的标准方程的求法,直线与抛物线的位置关系的应用,四边形面积的最值以及基本不等式的应用,考查转化思想以及计算能力.


科目:高中数学 来源: 题型:选择题
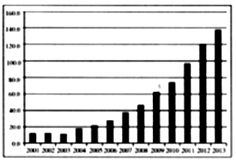 2001年至2013年北京市电影放映场次的情况如图所示.下列函数模型中,最不合适近似描述这13年间电影放映场次逐年变化规律的是( )
2001年至2013年北京市电影放映场次的情况如图所示.下列函数模型中,最不合适近似描述这13年间电影放映场次逐年变化规律的是( )| A. | y=ax2+bx+c | B. | y=aex+b | C. | y=aax+b | D. | y=alnx+b |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 212-57 | B. | 211-47 | C. | 210-38 | D. | 29-30 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
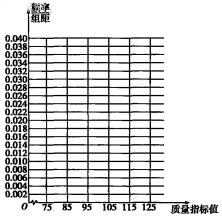 从某企业生产的某种产品中随机抽取100件,测量这些产品的某项质量指标,由测量结果得到如下频数分布表:
从某企业生产的某种产品中随机抽取100件,测量这些产品的某项质量指标,由测量结果得到如下频数分布表:| 质量指标值分组 | [75,85) | [85,95) | [95,105) | [105,115) | [115,125) |
| 频数 | 6 | 26 | 38 | 22 | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
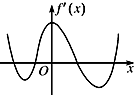
| A. | 无极大值点,有四个极小值点 | B. | 有三个极大值点,两个极小值点 | ||
| C. | 有两个极大值点,两个极小值点 | D. | 有四个极大值点,无极小值点 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com