
分析 (1)利用二次函数的性质知定点纵坐标为$\frac{3}{4}$,再有条件f(x+1)=f(-x),得出a,b的值;
(2)对a进行分类讨论:当a=0时,f(x)=-x+1,m≥1;再对对称轴进行讨论,当$\frac{a+1}{2a}$<2时,即a>$\frac{1}{3}$;当$\frac{a+1}{2a}$≥2时,即a≤$\frac{1}{3}$,分别去求|f(x)|的最大值.
解答 解:(1)∵函数f(x)的值域为[$\frac{3}{4}$,+∞),
∴4a-b2=3a,
∵f(x+1)=f(-x),
∴(2a-b)x+a-b=bx,
∴a=b=1,
∴f(x)=x2-x+1;
(2)当b=a+1,
f(x)=ax2-(a+1)x+1,f(x)恒过点(0,1);
当a=0时,f(x)=-x+1,
m≥|f(x)|恒成立,
∴m≥1;
0<a≤1,开口向上,对称轴$\frac{a+1}{2a}$≥1,
f(x)=ax2-(a+1)x+1=a(x-$\frac{a+1}{2a}$)2+1-$\frac{(a+1)^{2}}{4a}$,
①当a=1时f(x)=x2-2x+1,|f(x)|在x∈[0,2]的值域为[0,1];
要m≥|f(x)|,则m≥1;
②当0<a<1时,
根据对称轴分类:
当x=$\frac{a+1}{2a}$<2,即$\frac{1}{3}<a<1$,
△=(a-1)2>0,
f($\frac{a+1}{2a}$)=$\frac{1}{2}$-$\frac{1}{4}$($a+\frac{1}{a}$)∈(-$\frac{1}{3}$,0),又f(2)=2a-1<1,所以|f(x)|≤1;
当x=$\frac{a+1}{2a}$≥2,即0$<a≤\frac{1}{3}$;
f(x)在x∈[0,2]的最小值为f(2)=2a-1;
-1$<2a-1≤-\frac{1}{3}$,所以|f(x)|≤1,
综上所述,要对任意x∈[0,2]都有m≥|f(x)|恒成立,有m≥1
∴m≥1.
点评 考查了二次函数的性质和对二次函数对称轴的分类讨论求闭区间的最值问题.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{CN}$ | B. | $\overrightarrow{BC}$ | C. | $\overrightarrow{C{C}_{1}}$ | D. | $\overrightarrow{{B}{C}_{1}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
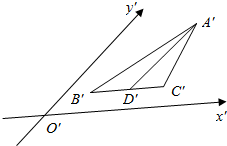 如图所示的水平放置的三角形的直观图中,D′是△A′B′C′中B′C′边的中点,那么A′B′,A′D′,A′C′三条线段对应原图形中线段AB,AD,AC中( )
如图所示的水平放置的三角形的直观图中,D′是△A′B′C′中B′C′边的中点,那么A′B′,A′D′,A′C′三条线段对应原图形中线段AB,AD,AC中( )| A. | 最长的是AB,最短的是AC | B. | 最长的是AC,最短的是AB | ||
| C. | 最长的是AB,最短的是AD | D. | 最长的是AD,最短的是AC |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ①③ | C. | ②③ | D. | ①②③ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com