
【题目】已知函数f(x)=(2x+b)ex , F(x)=bx﹣lnx,b∈R.
(1)若b<0,且存在区间M,使f(x)和F(x)在区间M上具有相同的单调性,求b的取值范围;
(2)若F(x+1)>b对任意x∈(0,+∞)恒成立,求b的取值范围.
【答案】
(1)解:f(x)=(2x+b)ex,f′(x)=(2x+b+2)ex,
∴当x∈(﹣∞,﹣ ![]() )时,f′(x)<0,当x∈(﹣
)时,f′(x)<0,当x∈(﹣ ![]() ,+∞)时,f′(x)>0,
,+∞)时,f′(x)>0,
∴f(x)的减区间为(﹣∞,﹣ ![]() ),增区间为(﹣
),增区间为(﹣ ![]() ,+∞).
,+∞).
F(x)的定义域为(0,+∞),且F′(x)=b﹣ ![]() .
.
∵b<0,∴F′(x)<0,则F(x)在定义域(0,+∞)上为减函数,
要使存在区间M,使f(x)和F(x)在区间M上具有相同的单调性,
则 ![]() >0,即b<﹣2.
>0,即b<﹣2.
∴b的取值范围是(﹣∞,﹣2)
(2)解:F(x+1)=b(x+1)﹣ln(x+1).
要使F(x+1)>b对任意x∈(0,+∞)恒成立,即bx﹣ln(x+1)>0对任意x∈(0,+∞)恒成立,
令g(x)=bx﹣ln(x+1),则g′(x)=b﹣ ![]() (x>0).
(x>0).
若b≤0,则g′(x)<0,g(x)在(0,+∞)上为减函数,而g(0)=0,不合题意;
若0<b<1,则当x∈(0, ![]() )时,g′(x)<0,当x∈(
)时,g′(x)<0,当x∈( ![]() ,+∞)时,g′(x)>0,
,+∞)时,g′(x)>0,
∴ ![]() =1﹣b+lnb>0,得b∈;
=1﹣b+lnb>0,得b∈;
若b≥1,则 ![]() ,g′(x)>0在(0,+∞)恒成立,
,g′(x)>0在(0,+∞)恒成立,
g(x)在(0,+∞)上为增函数,g(x)>g(0)=0.
综上,b的取值范围是[1,+∞)
【解析】(1)求出函数f(x)的导函数,由导函数的符号求得函数的单调区间,再求出函数F(x)的导函数,由b<0,可得F′(x)<0,则F(x)在定义域(0,+∞)上为减函数,要使存在区间M,使f(x)和F(x)在区间M上具有相同的单调性,需 ![]() >0,求解可得b的范围;(2)由F(x+1)>b对任意x∈(0,+∞)恒成立,可得bx﹣ln(x+1)>0对任意x∈(0,+∞)恒成立,令g(x)=bx﹣ln(x+1),求导可得b≤0时,g′(x)<0,g(x)在(0,+∞)上为减函数,而g(0)=0,不合题意;0<b<1时,
>0,求解可得b的范围;(2)由F(x+1)>b对任意x∈(0,+∞)恒成立,可得bx﹣ln(x+1)>0对任意x∈(0,+∞)恒成立,令g(x)=bx﹣ln(x+1),求导可得b≤0时,g′(x)<0,g(x)在(0,+∞)上为减函数,而g(0)=0,不合题意;0<b<1时, ![]() =1﹣b+lnb>0,得b∈;b≥1时,g(x)在(0,+∞)上为增函数,g(x)>g(0)=0成立,从而可得b的取值范围.
=1﹣b+lnb>0,得b∈;b≥1时,g(x)在(0,+∞)上为增函数,g(x)>g(0)=0成立,从而可得b的取值范围.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】如图,在直四棱柱![]() 中,底面
中,底面![]() 是边长为2的正方形,
是边长为2的正方形, ![]() 分别为线段
分别为线段![]() ,
, ![]() 的中点.
的中点.
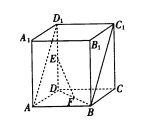
(1)求证: ![]() ||平面
||平面![]() ;
;
(2)四棱柱![]() 的外接球的表面积为
的外接球的表面积为![]() ,求异面直线
,求异面直线![]() 与
与![]() 所成的角的大小.
所成的角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学用“五点法”画函数![]()
![]() 在某一周期内的图象时,列表并填入了部分数据,如下表:
在某一周期内的图象时,列表并填入了部分数据,如下表:
| 0 |
|
|
|
|
|
|
| |||
| 0 | 2 | 0 | 0 |
(Ⅰ)请将上表数据补充完整,函数![]() 的解析式
的解析式![]() (直接写出结果即可)
(直接写出结果即可)
(Ⅱ)求函数![]() 的单调递增区间;/span>
的单调递增区间;/span>
(Ⅲ)求函数![]() 在区间
在区间![]() 上的最大值和最小值.
上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市由甲、乙两家乒乓球俱乐部,两家设备和服务都很好,但收费方式不同,甲家每张球台每小时5元;乙家按月计费,一个月中![]() 小时以内(含
小时以内(含![]() 小时)每张球台
小时)每张球台![]() 元,超过
元,超过![]() 小时的部分每张球台每小时
小时的部分每张球台每小时![]() 元.某公司准备下个月从两家中的一家租一张球台开展活动,活动时间不少于
元.某公司准备下个月从两家中的一家租一张球台开展活动,活动时间不少于![]() 小时,也不超过
小时,也不超过![]() 小时,设在甲家租一张球台开展活动
小时,设在甲家租一张球台开展活动![]() 小时的收费为
小时的收费为![]() 元,在乙家租一张球台开展活动
元,在乙家租一张球台开展活动![]() 小时的收费为
小时的收费为![]() 元.
元.
(1)试分别写出![]() 与
与![]() 的解析式;
的解析式;
(2)选择哪家比较合算?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设△ABC内角A,B,C所对的边分别为a,b,c,且 ![]() .
.
(1)若 ![]() ,求△ABC的面积;
,求△ABC的面积;
(2)若 ![]() ,
, ![]() ,且c>b,BC边的中点为D,求AD的长.
,且c>b,BC边的中点为D,求AD的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在R上的奇函数,且当x∈(0,+∞)时,f(x)=2018x+log2018x,则函数f(x)的零点个数是( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若二次函数f(x)=ax2+bx+c(a、b∈R)满足f(x+1)﹣f(x)=2x,且f(0)=1.
(1)求f(x)的解析式;
(2)若在区间[﹣1,﹣1]上,不等式f(x)>2x+m恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(2x+b)ex , F(x)=bx﹣lnx,b∈R.
(1)若b<0,且存在区间M,使f(x)和F(x)在区间M上具有相同的单调性,求b的取值范围;
(2)若F(x+1)>b对任意x∈(0,+∞)恒成立,求b的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com