
【题目】从某居民区随机抽取10个家庭,获得第i个家庭的月收入xi(单位:千元)与月储蓄yi(单位:千元)的数据资料,算得![]() =80,
=80, ![]() =20,
=20, ![]() =184,
=184, ![]() =720.
=720.
(Ⅰ)求家庭的月储蓄y对月收入x的线性回归方程y=bx+a;
(Ⅱ)判断变量x与y之间是正相关还是负相关;
(Ⅲ)若该居民区某家庭月收入为7千元,预测该家庭的月储蓄.
【答案】(Ⅰ)y=0.3x-0.4(Ⅱ)正相关(Ⅲ)1.7
【解析】
试题分析:(1)利用已知条件求出,样本中心坐标,利用参考公式求出b,a,然后求出线性回归方程y=bx+a;
(2)通过x=7,利用回归直线方程,推测该家庭的月储蓄
试题解析:(Ⅰ)由题意知n=10, ![]() =
=![]() =
=![]() =8,
=8, ![]() =
=![]() =
=![]() =2,
=2,
又lxx=![]() -n
-n ![]() 2=720-10×82=80, lxy=
2=720-10×82=80, lxy=![]() -n
-n ![]()
![]() =184-10×8×2=24,[来
=184-10×8×2=24,[来
由此得b=![]() =
=![]() =0.3, a=
=0.3, a=![]() -b
-b ![]() =2-0.3×8=-0.4,
=2-0.3×8=-0.4,
故所求线性回归方程为y=0.3x-0.4.
(Ⅱ)由于变量y的值随x值的增加而增加(b=0.3>0),故x与y之间是正相关.
(Ⅲ)将x=7代入回归方程可以预测该家庭的月储蓄为y=0.3×7-0.4=1.7(千元).


科目:高中数学 来源: 题型:
【题目】已知直线l1经过两点(-1,-2),(-1,4),直线l2经过两点(2,1),(6,y),且l1⊥l2,则y=( )
A. -2 B. 1 C. 2 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方体ABCD﹣A1B1C1D1的棱长为1,线段B1D1上有两个动点E,F,且EF=![]() ,则下列结论中错误的是( )
,则下列结论中错误的是( )
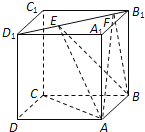
A.AC⊥BE
B.EF∥平面ABCD
C.三棱锥A﹣BEF的体积为定值
D.异面直线AE,BF所成的角为定值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个年级有12个班,每个班有50名同学,随机编号为1~50,为了了解他们在课外的兴趣,要求每班第40号同学留下来进行问卷调查,这里运用的抽样方法是( )
A. 抽签法 B. 分层抽样法
C. 随机数表法 D. 系统抽样法
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校甲、乙两个班各派10名同学参加英语口语比赛,并记录他们的成绩,得到如图所示的茎叶图.现拟定在各班中分数超过本班平均分的同学为“口语王”.
(1)记甲班“口语王”人数为![]() ,乙班“口语王”人数为
,乙班“口语王”人数为![]() ,比较
,比较![]() ,
,![]() 的大小.
的大小.
(2)随机从“口语王”中选取2人,记![]() 为来自甲班“口语王”的人数,求
为来自甲班“口语王”的人数,求![]() 的分布列和数学期望.
的分布列和数学期望.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() ,过其焦点
,过其焦点![]() 作两条相互垂直且不平行于坐标轴的直线,它们分别交抛物线
作两条相互垂直且不平行于坐标轴的直线,它们分别交抛物线![]() 于点
于点![]() 、
、![]() 和点
和点![]() 、
、![]() ,线段
,线段![]() 、
、![]() 的中点分别为
的中点分别为![]() 、
、![]() .
.
(Ⅰ)求线段![]() 的中点
的中点![]() 的轨迹方程;
的轨迹方程;
(Ⅱ)求![]() 面积的最小值;
面积的最小值;
(Ⅲ)过![]() 、
、![]() 的直线
的直线![]() 是否过定点?若是,求出定点坐标,若不是,请说明理由.
是否过定点?若是,求出定点坐标,若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某租赁公司拥有汽车100辆.当每辆车的月租金为3 000元时,可全部租出.当每辆车的月租金每增加50元时,未租出的车将会增加一辆.租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元.
(1)当每辆车的月租金定为3 600元时,能租出多少辆车?
(2)当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com