
【题目】已知函数![]()
(1)讨论函数![]() 的单调性;
的单调性;
(2)设![]() ,当函数
,当函数![]() 与
与![]() 的图象有三个不同的交点时,求实数
的图象有三个不同的交点时,求实数![]() 的取值范围.
的取值范围.
【答案】(1) 函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
(2) ![]()
【解析】
(1)对函数![]() 求导,根据
求导,根据![]() 的不同取值,结合不等式,可以判断出函数的单调性;
的不同取值,结合不等式,可以判断出函数的单调性;
(2)由题意可知:![]() ,得
,得![]() .得
.得![]() ,
,
设![]() ,则
,则![]() 有三个不同的根等价于函数
有三个不同的根等价于函数![]() 存在三个不同的零点.对函数
存在三个不同的零点.对函数![]() 进行求导,然后判断出其单调性,结合零点存在原理,最后求出实数
进行求导,然后判断出其单调性,结合零点存在原理,最后求出实数![]() 的取值范围.
的取值范围.
(1)![]() 的定义域是
的定义域是![]() ,
,
![]() ,
,
当![]() 时.
时.![]() 两数
两数![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,令
时,令![]() ,得
,得![]() ;令
;令![]() ,得
,得![]() .
.
故函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单洞递破.
上单洞递破.
(2)由![]() ,得
,得![]() .得
.得![]() ,
,
设![]() ,则
,则![]() 有三个不同的根等价于函数
有三个不同的根等价于函数![]() 存在三个不同的零点.
存在三个不同的零点.
![]() ,
,
当![]() 即
即![]() 时,
时,![]() ,
,![]() 单调递减,不可能有三个不同的零点,
单调递减,不可能有三个不同的零点,
当![]() 即
即![]() ,
,![]() 有两个零点
有两个零点![]() ,
,
![]() ,
,
又![]() 开口向下,
开口向下,
当![]() 时,
时, ![]() ,函数
,函数![]() 在
在![]() 上单调递诫:
上单调递诫:
当![]() 时.
时.![]() 函数
函数![]() 在
在![]() 上单调递增:
上单调递增:
当![]() 时.
时.![]() ,函数
,函数![]() 在
在![]() 上单调递减.
上单调递减.
因为![]() ,又
,又![]() ,有
,有![]() ,
,
所以![]()
 ,
,
令![]() .则
.则![]() .
.
令![]() .则
.则![]() 单调递增.
单调递增.
由![]() ,求得
,求得![]() ,
,
当![]() 时,
时,![]() 单调递减,
单调递减,![]() .,
.,
显然在![]() 上单调递增,
上单调递增,
故![]() .
.
由零点存在性定理知![]() 在区间
在区间![]() 上有一个根.设为
上有一个根.设为![]() ,
,
又 .得
.得 .所以
.所以![]() .所以
.所以![]() 是
是![]() 的另一个零点,
的另一个零点,
故当![]() 时,
时,![]() 存在三个不同的零点
存在三个不同的零点![]() .
.
故实数![]() 的取值范围是
的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】某地拟规划种植一批芍药,为了美观,将种植区域(区域I)设计成半径为1km的扇形![]() ,中心角
,中心角![]() (
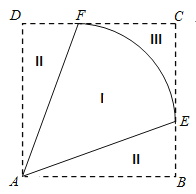
(![]() ).为方便观赏,增加收入,在种植区域外围规划观赏区(区域II)和休闲区(区域III),并将外围区域按如图所示的方案扩建成正方形
).为方便观赏,增加收入,在种植区域外围规划观赏区(区域II)和休闲区(区域III),并将外围区域按如图所示的方案扩建成正方形![]() ,其中点
,其中点![]() ,
,![]() 分别在边
分别在边![]() 和
和![]() 上.已知种植区、观赏区和休闲区每平方千米的年收入分别是10万元、20万元、20万元.
上.已知种植区、观赏区和休闲区每平方千米的年收入分别是10万元、20万元、20万元.
(1)要使观赏区的年收入不低于5万元,求![]() 的最大值;
的最大值;
(2)试问:当![]() 为多少时,年总收入最大?
为多少时,年总收入最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() .
.
(1)过点![]() 的直线
的直线![]() 与抛物线
与抛物线![]() 相交于
相交于![]() 两点,若
两点,若![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)点![]() 是抛物线
是抛物线![]() 上的两点,点
上的两点,点![]() 的纵坐标分别为1,2,分别过点
的纵坐标分别为1,2,分别过点![]() 作倾斜角互补的两条直线交抛物线
作倾斜角互补的两条直线交抛物线![]() 于另外不同两点
于另外不同两点![]() ,求直线
,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据阅兵领导小组办公室介绍,2019年国庆70周年阅兵有59个方(梯)队和联合军乐团,总规模约1.5万人,是近几次阅兵中规模最大的一次.其中,徒步方队15个.为了保证阅兵式时队列保持整齐,各个方队对受阅队员的身高也有着非常严格的限制,太高或太矮都不行.徒步方队队员,男性身高普遍在175cm至185cm之间;女性身高普遍在163cm至175cm之间,这是常规标准.要求最为严格的三军仪仗队,其队员的身高一般都在184cm至190cm之间.经过随机调查某个阅兵阵营中女子100人,得到她们身高的直方图,如图,记C为事件:“某一阅兵女子身高不低于169cm”,根据直方图得到P(C)的估计值为0.5.
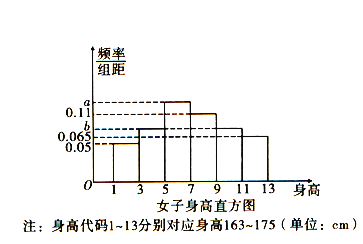
(1)求直方图中a,b的值;
(2)估计这个阵营女子身高的平均值 (同一组中的数据用该组区间的中点值为代表)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】垃圾种类可分为可回收垃圾、干垃圾、湿垃圾、有害垃圾等,为调查中学生对垃圾分类的了解程度,某调查小组随机从本市一中高一的![]() 名学生(其中女生
名学生(其中女生![]() 人)中,采用分层抽样的方法抽取
人)中,采用分层抽样的方法抽取![]() 名学生进行调查,已知抽取的
名学生进行调查,已知抽取的![]() 名学生中有男生
名学生中有男生![]() 人、
人、
(1)求![]() 值及抽到的女生人数;
值及抽到的女生人数;
(2)调查小组请这![]() 名学生指出生活中若干项常见垃圾的种类,把能准确分类不少于
名学生指出生活中若干项常见垃圾的种类,把能准确分类不少于![]() 项的称为“比较了解”,少于三项的称为“不太了解”,调查结果如下:
项的称为“比较了解”,少于三项的称为“不太了解”,调查结果如下:
0项 | 1项 | 2项 | 3项 | 4项 | 5项 | 5项以上 | |
男生(人) | 4 | 22 | 34 | 18 | 16 | 10 | 6 |
女生(人) | 0 | 15 | 20+m | 20 | 16 | 9 | m |
求![]() 值,完成如下
值,完成如下![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为学生对垃圾分类的了解程度与性别有关?
的把握认为学生对垃圾分类的了解程度与性别有关?
不太了解 | 比较了解 | 合计 | |
男生 | |||
女生 | |||
合计 |
(3)在(2)条件下,从抽取的“比较了解”的学生中仍采用分层抽样的方法抽取![]() 名.再从这
名.再从这![]() 名学生中随机抽取
名学生中随机抽取![]() 人作义务讲解员,求抽取的
人作义务讲解员,求抽取的![]() 人中至少一名女生的概率.
人中至少一名女生的概率.
参考数据:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
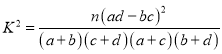 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱锥![]() 中,底面
中,底面![]() 是边长为6的正三角形,
是边长为6的正三角形,![]() 底面
底面![]() ,且
,且![]() 与底面
与底面![]() 所成的角为
所成的角为![]() .
.
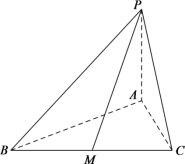
(1)求三棱锥![]() 的体积;
的体积;
(2)若![]() 是
是![]() 的中点,求异面直线
的中点,求异面直线![]() 与
与![]() 所成角的大小(结果用反三角函数值表示).
所成角的大小(结果用反三角函数值表示).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有![]() 行数表如下:
行数表如下:
第一行:![]()
第二行:![]()
第三行:![]()
…… …… ……
第![]() 行:
行:![]()
第m行:![]()
按照上述方式从第一行写到第m行(写下的第n个数记作![]() )得到有穷数列
)得到有穷数列![]() ,其前n项和为
,其前n项和为![]() ,若
,若![]() 存在,则
存在,则![]() 的最小值为______
的最小值为______
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着手机的发展,“微信”逐渐成为人们交流的一种形式.某机构对“使用微信交流”的态度进行调查,随机抽取了50人,他们年龄的频数分布及对“使用微信交流”赞成人数如下表.
年龄 (单位:岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75] |
频数 | 5 | 10 | 15 | 10 | 5 | 5 |
赞成人数 | 5 | 10 | 12 | 7 | 2 | 1 |
(1)若以“年龄45岁为分界点”,由以上统计数据完成下面2×2列联表,并判断是否有99%的把握认为“使用微信交流”的态度与人的年龄有关;
年龄不低于45岁的人数 | 年龄低于45岁的人数 | 合计 | |
赞成 | |||
不赞成 | |||
合计 |
(2)若从年龄在[55,65)的被调查人中随机选取2人进行追踪调查,求2人中至少有1人不赞成“使用微信交流”的概率.
参考数据:
P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
K2=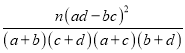 ,其中n=a+b+c+d.
,其中n=a+b+c+d.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com