
【题目】定义在(﹣1,1)上的奇函数f(x)是减函数满足f(1﹣a)+f(1﹣2a)<0,则a的取值范围是 .
【答案】(0, ![]() )
)
【解析】解:由于定义在(﹣1,1)上的奇函数f(x)是减函数,满足f(1﹣a)+f(1﹣2a)<0,
故有 f(1﹣a)<﹣f(1﹣2a)=f(2a﹣1),
∴ 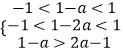 ,
,
解得 0<a< ![]() ,故a的取值范围是(0,
,故a的取值范围是(0, ![]() ).
).
所以答案是:(0, ![]() ).
).
【考点精析】掌握函数单调性的性质和函数奇偶性的性质是解答本题的根本,需要知道函数的单调区间只能是其定义域的子区间 ,不能把单调性相同的区间和在一起写成其并集;在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇.


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:高中数学 来源: 题型:
【题目】为考察高中生的性别与喜欢数学课程之间的关系,在某学校高中生中随机抽取了250名学生,得到如图的二维条形图.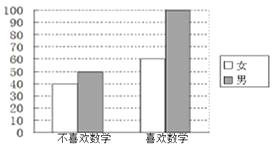
(1)根据二维条形图,完成下表:
男 | 女 | 合计 | |
喜欢数学课程 | |||
不喜欢数学课程 | |||
合计 |
(2)对照如表,利用列联表的独立性检验估计,请问有多大把握认为“性别与喜欢数学有关系”?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-5:不等式选讲]
已知函数f(x)=|2x﹣1|+|x+1|,g(x)=|x﹣a|+|x+a|.
(Ⅰ)解不等式f(x)>9;
(Ⅱ)x1∈R,x2∈R,使得f(x1)=g(x2),求实数a的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx+a(x﹣1)2,其中a>0.
(1)当a=1时,求曲线y=f(x)在点(1,f(1))处的切线方程;(2)讨论函数f(x)的单调性;
(3)若函数f(x)有两个极值点x1,x2,且x1<x2,求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,△ABC内接于☉O,AB=AC,直线MN切☉O于点C,弦BD∥MN,AC与BD相交于点E. 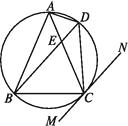
(1)求证:△ABE≌△ACD;
(2)求证:BE=BC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,圆锥SO的轴截面△SAB是边长为4的正三角形,M为母线SB的中点,过直线AM作平面β⊥面SAB,设β与圆锥侧面的交线为椭圆C,则椭圆C的短半轴长为( ) 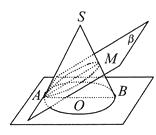
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是网络工作者经常用来解释网络运作的蛇形模型:数字1出现在第1行;数字2,3出现在第2行;数字6,5,4(从左至右)出现在第3行;数字7,8,9,10出现在第4行,依此类推,則第20行从左至右的第4个数字应是 . 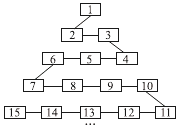
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com