
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,以椭圆
,以椭圆![]() 的长轴和短轴为对角线的四边形的面积为
的长轴和短轴为对角线的四边形的面积为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
,![]() 两点,设
两点,设![]() 为椭圆
为椭圆![]() 上一动点,且满足
上一动点,且满足![]() (
(![]() 为坐标原点).当
为坐标原点).当![]() 时,求
时,求![]() 的最大值.
的最大值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)根据所给离心率及四边形面积,结合椭圆中![]() ,解方程组即可确定
,解方程组即可确定![]() 的值,进而得椭圆
的值,进而得椭圆![]() 的方程;
的方程;
(2)设![]() ,将直线方程与椭圆方程联立,由判别式
,将直线方程与椭圆方程联立,由判别式![]() 可确定
可确定![]() 的范围;由韦达定理可表示出
的范围;由韦达定理可表示出![]() ,将
,将![]() 代入直线方程可表示出
代入直线方程可表示出![]() .由平面向量的坐标运算,表示出点
.由平面向量的坐标运算,表示出点![]() 的坐标,代入椭圆方程即可建立
的坐标,代入椭圆方程即可建立![]() 与
与![]() 的关系式,由
的关系式,由![]() 进一步确定
进一步确定![]() 的取值范围即可.
的取值范围即可.
(1)椭圆![]() 的离心率为
的离心率为![]() ,则
,则![]() ,
,
以椭圆![]() 的长轴和短轴为对角线的四边形的面积为
的长轴和短轴为对角线的四边形的面积为![]() ,则
,则![]() ,
,
再有![]() ,
,
联立上述等式可得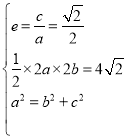 ,解得
,解得![]() ,
,
所以椭圆的标准方程为![]() .
.
(2)直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
,![]() 两点,设
两点,设![]() ,
,
则联立直线与椭圆方程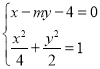 ,化简可得
,化简可得![]() ,
,
则![]() ,
,
可知![]() ,
,
解得![]() 或
或![]() ;
;
而![]()
所以![]() ,
,
因为![]() ,
,
所以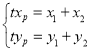 ,代入可得
,代入可得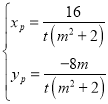
因为点P在椭圆上,
代入可得 ,化简可得
,化简可得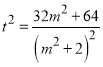 ,
,
因为![]() ,
,
所以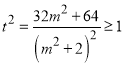 ,化简可得
,化简可得![]() ,
,
所以![]() ,即
,即![]() ,
,
又因为![]() 或
或![]() ;
;
所以![]()


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ln![]() .
.
(1)求函数f(x)的定义域,并判断函数f(x)的奇偶性;
(2)对于x∈[2,6],f(x)=ln![]() >ln
>ln![]() 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地级市共有![]() 中小学生,其中有
中小学生,其中有![]() 学生在
学生在![]() 年享受了“国家精准扶贫”政策,在享受“国家精准扶贫”政策的学生中困难程度分为三个等次:一般困难、很困难、特别困难,且人数之比为
年享受了“国家精准扶贫”政策,在享受“国家精准扶贫”政策的学生中困难程度分为三个等次:一般困难、很困难、特别困难,且人数之比为![]() ,为进一步帮助这些学生,当地市政府设立“专项教育基金”,对这三个等次的困难学生每年每人分别补助
,为进一步帮助这些学生,当地市政府设立“专项教育基金”,对这三个等次的困难学生每年每人分别补助![]() 元、
元、![]() 元、
元、![]() 元,经济学家调查发现,当地人均可支配年收入较上一年每增加
元,经济学家调查发现,当地人均可支配年收入较上一年每增加![]() ,一般困难的学生中有
,一般困难的学生中有![]() 会脱贫,脱贫后将不再享受“精准扶贫”政策,很困难的学生中有
会脱贫,脱贫后将不再享受“精准扶贫”政策,很困难的学生中有![]() 转为一般困难,特别困难的学生中有
转为一般困难,特别困难的学生中有![]() 转为很困难.现统计了该地级市
转为很困难.现统计了该地级市![]() 年到
年到![]() 年共
年共![]() 年的人均可支配年收入,对数据初步处理后得到了如图所示的散点图和表中统计量的值,其中年份
年的人均可支配年收入,对数据初步处理后得到了如图所示的散点图和表中统计量的值,其中年份![]() 取
取![]() 时代表
时代表![]() 年,
年,![]() 与
与![]() (万元)近似满足关系式
(万元)近似满足关系式![]() ,其中
,其中![]() ,
,![]() 为常数.(
为常数.(![]() 年至
年至![]() 年该市中学生人数大致保持不变)
年该市中学生人数大致保持不变)
|
|
|
|
|
|
|
|
|
|
|
|
其中![]() ,
,![]()
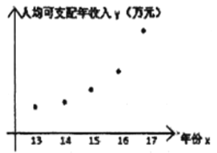
(1)估计该市![]() 年人均可支配年收入;
年人均可支配年收入;
(2)求该市![]() 年的“专项教育基金”的财政预算大约为多少?
年的“专项教育基金”的财政预算大约为多少?
附:对于一组具有线性相关关系的数据![]() ,
,![]() ,
,![]() ,
,![]() ,其回归直线方程
,其回归直线方程![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为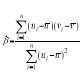 ,
,![]()
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班随机抽查了![]() 名学生的数学成绩,分数制成如图的茎叶图,其中
名学生的数学成绩,分数制成如图的茎叶图,其中![]() 组学生每天学习数学时间不足
组学生每天学习数学时间不足![]() 个小时,
个小时,![]() 组学生每天学习数学时间达到一个小时,学校规定
组学生每天学习数学时间达到一个小时,学校规定![]() 分及
分及![]() 分以上记为优秀,
分以上记为优秀,![]() 分及
分及![]() 分以上记为达标,
分以上记为达标,![]() 分以下记为未达标.
分以下记为未达标.
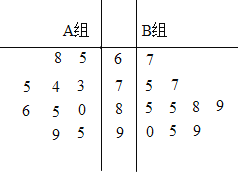
(1)根据茎叶图完成下面的列联表:
达标 | 未达标 | 总计 | |
| |||
| |||
总计 |
(2)判断是否有![]() 的把握认为“数学成绩达标与否”与“每天学习数学时间能否达到一小时”有关.
的把握认为“数学成绩达标与否”与“每天学习数学时间能否达到一小时”有关.
参考公式与临界值表: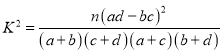 ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 满足
满足![]() ,
,![]() ,
,![]() .
.
(1)若![]() ,试问是否存在实数
,试问是否存在实数![]() ,使得数列
,使得数列![]() 是等比数列?若存在,求出
是等比数列?若存在,求出![]() 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(2)在(1)的条件下,求数列![]() 的通项公式.
的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)已知在四棱锥![]() 中,底面
中,底面![]() 是矩形,且
是矩形,且![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,![]() 分别是线段
分别是线段![]() ,
,![]() 的中点.
的中点.
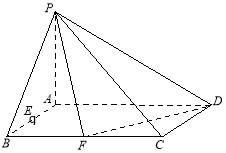
(1)判断并说明![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不
的值;若不
存在,请说明理由;
(2)若![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,求二面角
,求二面角![]() 的平面角的余弦值.
的平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】交大设计学院植物园准备用一块边长为4百米的等边ΔABC田地(如图)建立芳香植物生长区、植物精油提炼处与植物精油体验点.田地内拟建笔直小路MN、AP,其中M、N分别为AC、BC的中点,点P在CN上.规划在小路MN和AP的交点O(O与M、N不重合)处设立植物精油体验点,图中阴影部分为植物精油提炼处,空白部分为芳香植物生长区,A、N为出入口(小路宽度不计).为节约资金,小路MO段与OP段建便道,供芳香植物培育之用,费用忽略不计,为车辆安全出入,小路AO段的建造费用为每百米4万元,小路ON段的建造费用为每百米3万元.
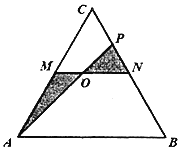
(1)若拟建的小路AO段长为![]() 百米,求小路ON段的建造费用;
百米,求小路ON段的建造费用;
(2)设∠BAP=![]() ,求
,求![]() 的值,使得小路AO段与ON段的建造总费用最小,并求岀最小建造总费用(精确到元).
的值,使得小路AO段与ON段的建造总费用最小,并求岀最小建造总费用(精确到元).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com