
【题目】如图所示,在四棱锥E-ABCD中,平面ABCD⊥平面AEB,且四边形ABCD为矩形.∠BAE=90°,AE=4,AD=2,F,G,H分别为BE,AE,AD的中点.
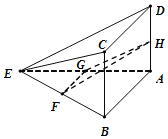
(Ⅰ)求证:CD∥平面FGH;
(Ⅱ)求证:平面FGH⊥平面ADE;
(Ⅲ)在线段DE求一点P,使得AP⊥FH,并求出AP的值.
【答案】(Ⅰ)见解析;(Ⅱ)见解析;(Ⅲ)![]()
【解析】
(Ⅰ)根据三角形中位线性质以及矩形性质得CD∥FG,再根据线面平行判定定理得结论,(Ⅱ)先根据线面垂直判定定理得AB⊥平面ADE,再根据平行得GF⊥平面ADE,最后根据面面垂直判定定理得结论,(Ⅲ)作AP⊥DE于P,再根据线面垂直判定与性质定理得AP⊥FH,再根据面面垂直性质定理得AE⊥平面ABCD,即得AE⊥AD,最后根据直角三角形解得AP的值.
(Ⅰ)证明:在矩形ABCD中,CD∥AB,
∵F,G分别为BE,AE的中点,∴FG∥AB,∴CD∥FG,
∵CD![]() 平面FGH,FG平面FGH,
平面FGH,FG平面FGH,
∴CD∥平面FGH.
(Ⅱ)证明:在矩形ABCD中,AD⊥AB,又∵∠BAE=90°,∴AB⊥AE,又AD∩AE=A
∴AB⊥平面ADE,又GF∥AB∴GF⊥平面ADE,
∵GF平面FGH,∴平面FGH⊥平面ADE.
(Ⅲ)作AP⊥DE于P,∵GF⊥平面ADE,且AP平面ADE,∴GF⊥AP,
∵G,H分别为AE,AD的中点,∴GH∥DE, ∵AP⊥DE∴GH⊥AP
∵GF∩GH=G,∴AP⊥平面FGH,
∵FH平面FGH,∴AP⊥FH,
∵矩形ABCD⊥平面AEB,且平面ABCD∩平面AEB=AB,
∴AE⊥平面ABCD,∴AE⊥AD,
在直角三角形AED中,AE=4,AD=2,可求得![]() .故AP的值为:
.故AP的值为:![]() .
.



 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:高中数学 来源: 题型:
【题目】某中学为了组建一支业余足球队,在高一年级随机选取50名男生测量身高,发现被测男生的身高全部在160cm到184cm之间,将测量结果按如下方式分成六组:第1组![]() ,第2组
,第2组![]() ,...,第6组
,...,第6组![]() ,如图是按上述分组得到的频率分布直方图,以频率近似概率.
,如图是按上述分组得到的频率分布直方图,以频率近似概率.
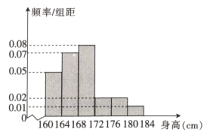
(1)若学校要从中选1名男生担任足球队长,求被选取的男生恰好在第5组或第6组的概率;
(2)现在从第5与第6组男生中选取两名同学担任守门员,求选取的两人中最多有1名男生来自第5组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,在区间
,在区间![]() 上有最大值
上有最大值![]() ,最小值
,最小值![]() ,设函数
,设函数![]() .
.
(1)求![]() 的值;
的值;
(2)不等式![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围;
的取值范围;
(3)方程![]() 有三个不同的实数解,求实数
有三个不同的实数解,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有下列四个命题:
(1)“若![]() ,则
,则![]() ,
,![]() 互为倒数”的逆命题;
互为倒数”的逆命题;
(2)“面积相等的三角形全等”的否命题;
(3)“若![]() ,则
,则![]() 无实数解”的否命题;
无实数解”的否命题;
(4)命题:“空间中到一个正四面体的六条棱所在的直线距离均相等的点有且只有![]() 个”; 其中真命题( )
个”; 其中真命题( )
A.(1)(2)B.(2)(3)C.(1)(2)(3)D.(1)(2)(4)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过点![]() 作互相垂直的直线
作互相垂直的直线![]() ,
,![]() ,
,![]() 交
交![]() 正半轴于
正半轴于![]() 点,
点,![]() 交
交![]() 正半轴于
正半轴于![]() 点,则线段
点,则线段![]() 中点
中点![]() 轨迹方程为_______________________;过原点
轨迹方程为_______________________;过原点![]() 与
与![]() 、
、![]() 、
、![]() 四点的圆半径的最小值为______________.
四点的圆半径的最小值为______________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com