
【题目】已知函数f(x)=![]() .
.
(1)求f(2)+f![]() ,f(3)+f
,f(3)+f![]() 的值;
的值;
(2)求证:f(x)+f![]() 是定值;
是定值;
(3)求f(2)+f![]() +f(3)+f
+f(3)+f![]() +…+
+…+![]() +f
+f![]() 的值.
的值.
 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() 过点
过点![]() ,其参数方程为
,其参数方程为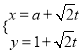 (
(![]() 为参数,
为参数, ![]() ),以
),以![]() 为极点,
为极点, ![]() 轴非负半轴为极轴,建立极坐标系,曲线
轴非负半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知曲线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,且
两点,且![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于定义域为![]() 的函数
的函数![]() ,若同时满足下列条件:
,若同时满足下列条件:
①![]() 在
在![]() 内单调递增或单调递减;
内单调递增或单调递减;
②存在区间![]() ,使
,使![]() 在
在![]() 上的值域为
上的值域为![]() ;那么把
;那么把![]() (
(![]() )叫闭函数.
)叫闭函数.
(1)求闭函数![]() 符合条件②的区间
符合条件②的区间![]() ;
;
(2)判断函数![]() 是否为闭函数?并说明理由;
是否为闭函数?并说明理由;
(3)判断函数![]() 是否为闭函数?若是闭函数,求实数
是否为闭函数?若是闭函数,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系下,已知曲线C1:ρ=cosθ+sinθ和曲线C2:ρsin(θ-![]() )=
)=![]() .
.
(1)求曲线C1和曲线C2的直角坐标方程;
(2)当θ∈(0,π)时,求曲线C1和曲线C2公共点的一个极坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了打好脱贫攻坚战,某贫困县农科院针对玉米种植情况进行调研,力争有效的改良玉米品种,为农民提供技术支.现对已选出的一组玉米的茎高进行统计,获得茎叶图如右图(单位:厘米),设茎高大于或等于180厘米的玉米为高茎玉米,否则为矮茎玉米.
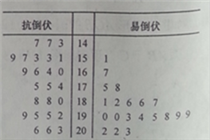 (1)完成列
(1)完成列![]() 联表,并判断是否可以在犯错误的概率不超过1%的前提下,认为抗倒伏与玉米矮茎有关?
联表,并判断是否可以在犯错误的概率不超过1%的前提下,认为抗倒伏与玉米矮茎有关?
(2)为了改良玉米品种,现采用分层抽样的方法从抗倒伏的玉米中抽出5株,再从这5株玉米中选取2株进行杂交试验,选取的植株均为矮茎的概率是多少?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】沪昆高速铁路全线2016年12月28日开通运营.途经鹰潭北站的![]() 、
、![]() 两列列车乘务组工作人员为了了解乘坐本次列车的乘客每月需求情况,分别在两个车次各随机抽取了100名旅客进行调查,下面是根据调查结果,绘制了月乘车次数的频率分布直方图和频数分布表.
两列列车乘务组工作人员为了了解乘坐本次列车的乘客每月需求情况,分别在两个车次各随机抽取了100名旅客进行调查,下面是根据调查结果,绘制了月乘车次数的频率分布直方图和频数分布表.
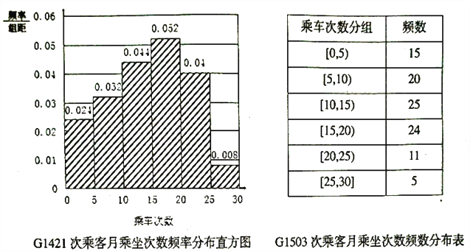
(1)若将频率视为概率,月乘车次数不低于15次的称之为“老乘客”,试问:哪一车次的“老乘客”较多,简要说明理由;
(2)已知在![]() 次列车随机抽到的50岁以上人员有35名,其中有10名是“老乘客”,由条件完成
次列车随机抽到的50岁以上人员有35名,其中有10名是“老乘客”,由条件完成![]() 列联表,并根据资料判断,是否有
列联表,并根据资料判断,是否有![]() 的把握认为年龄与乘车次数有关,说明理由.
的把握认为年龄与乘车次数有关,说明理由.
老乘客 | 新乘客 | 合计 | |
50岁以上 | |||
50岁以下 | |||
合计 |
附:随机变量![]() (其中
(其中![]() 为样本容量)
为样本容量)
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋子中有四个小球,分别写有“幸”“福”“快”“乐”四个字,有放回地从中任取一个小球,取到“快”就停止,用随机模拟的方法估计直到第二次停止的概率:先由计算器产生1到4之间取整数值的随机数,且用1,2,3,4表示取出小球上分别写有“幸”“福”“快”“乐”四个字,以每两个随机数为一组,代表两次的结果,经随机模拟产生了20组随机数:
13 24 12 32 43 14 24 32 31 21
23 13 32 21 24 42 13 32 21 34
据此估计,直到第二次就停止的概率为( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点
的右焦点![]() ,椭圆
,椭圆![]() 的左,右顶点分别为
的左,右顶点分别为![]() .过点
.过点![]() 的直线
的直线![]() 与椭圆交于
与椭圆交于![]() 两点,且
两点,且![]() 的面积是
的面积是![]() 的面积的3倍.
的面积的3倍.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)若![]() 与
与![]() 轴垂直,
轴垂直,![]() 是椭圆
是椭圆![]() 上位于直线
上位于直线![]() 两侧的动点,且满足
两侧的动点,且满足![]() ,试问直线
,试问直线![]() 的斜率是否为定值,请说明理由.
的斜率是否为定值,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com