Question

已知四棱锥P-ABCD的直观图（如图(1)）及左视图（如图(2)），底面ABCD是边长为2的正方形，平面PAB⊥平面ABCD，PA=PB。

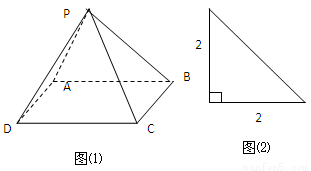
(1)求证：AD⊥PB；

(2)求异面直线PD与AB所成角的余弦值；

(3)求平面PAB与平面PCD所成锐二面角的大小.

 

Answer 1

【答案】

⑴利用面面垂直的性质得到线面垂直，然后再由线面垂直证得线线垂直；⑵；⑶。

【解析】

试题分析：⑴取AB的中点O，连接PO，因为PA=PB，则PO⊥AB，

又∵ 平面PAB⊥平面ABCD，平面PAB∩平面ABCD=AB，PO平面PAB，

∴PO⊥平面ABCD，∴PO⊥AD，    2分

而AD⊥AB，PO∩AB=O，∴AD⊥平面PAB，∴AD⊥PB。    4分

⑵过O作AD的平行线为x轴，以OB、OP所在直线分别为y、z轴，建立如图的空间直角坐标系，则A（0，-1，0），D（2，-1，0），B（0，1，0），C（2，1，0），

=（2，-1，-2），=（0，2，0），cos＜，＞==-，

即异面直线PD与AB所成角的余弦值为。    8分

⑶易得平面PAB的一个法向量为n=（1，0 ，0）。

设平面PCD的一个法向量为m=（x，y，z），由⑵知=（2，-1，-2），=（0，-2，0），则，即，解得x=z，

令x=1，则m=（1，0，1），   .10分

则cos＜n，m＞==，

即平面PAB与平面PCD所成锐二面角的大小为。    .12分

考点：本题考查了空间中线面关系

点评：空间各种角问题最终都可以转化为线线角求解，可用空间向量的数量积及其夹角余弦公式求解。