[题目]我国古代的天文学和数学著作中记载:一年有二十四个节气.每个节气晷长损益相同(晷是按照日影测定时刻的仪器.晷长即为所测量影子的长度)．二十四节气及晷长变化如图所示.相邻两个节气晷长的变化量相同.周而复始．若冬至晷长一丈三尺五寸.夏至晷长一尺五寸(一丈等于十尺.一尺等于十寸).则夏至之后的那个节气晷长是( ) A.五寸B.二尺五寸C.三尺五寸D 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】我国古代的天文学和数学著作《周髀算经》中记载：一年有二十四个节气，每个节气晷（guǐ）长损益相同（晷是按照日影测定时刻的仪器，晷长即为所测量影子的长度）．二十四节气及晷长变化如图所示，相邻两个节气晷长的变化量相同，周而复始．若冬至晷长一丈三尺五寸，夏至晷长一尺五寸（一丈等于十尺，一尺等于十寸），则夏至之后的那个节气（小暑）晷长是（）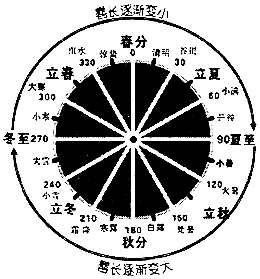
A.五寸
B.二尺五寸
C.三尺五寸
D.四尺五寸

【答案】A
【解析】解：设晷影长为等差数列{an}，公差为d，a1=135，a13=15，

则135+12d=15，解得d=﹣10．

∴a14=135﹣10×13=5

∴《易经》中所记录的惊蛰的晷影长是5寸．

故选：A．

【考点精析】解答此题的关键在于理解等差数列的通项公式（及其变式）的相关知识，掌握通项公式：或．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】某单位附近只有甲，乙两个临时停车场，它们各有50个车位，为了方便市民停车，某互联网停车公司对这两个停车场在工作日某些固定时刻的剩余停车位进行记录，如下表：

时间	8点	10点	12点	14点	16点	18点
停车场甲	10	3	12	6	12	17
停车场乙	13	4	3	2	6	19

如果表中某一时刻停车场剩余停车位数低于总车位数的10%，那么当车主驱车抵达单位附近时，该公司将会向车主发出停车场饱和警报．
（Ⅰ）假设某车主在以上六个时刻抵达单位附近的可能性相同，求他收到甲停车场饱和警报的概率；
（Ⅱ）从这六个时刻中任选一个时刻，求甲停车场比乙停车场剩余车位数少的概率；
（Ⅲ）当停车场乙发出饱和警报时，求停车场甲也发出饱和警报的概率．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】2017年3月27日，一则“清华大学要求从2017级学生开始，游泳达到一定标准才能毕业”的消息在体育界和教育界引起了巨大反响．游泳作为一项重要的求生技能和运动项目受到很多人的喜爱．其实，已有不少高校将游泳列为必修内容．某中学为了解2017届高三学生的性别和喜爱游泳是否有关，对100名高三学生进行了问卷调查，得到如下列联表：

	喜欢游泳	不喜欢游泳	合计
男生		10
女生	20
合计

已知在这100人中随机抽取1人，抽到喜欢游泳的学生的概率为．
（Ⅰ）请将上述列联表补充完整；
（Ⅱ）判断是否有99.9%的把握认为喜欢游泳与性别有关？
附：

p（K2≥k0）	0.10	0.05	0.025	0.010	0.005	0.001
k0	2.706	3.841	5.024	6.635	7.879	10.828

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】函数的图象不可能是（）
A.
B.
C.
D.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】在直角坐标系xOy中，设抛物线E：y2=2px（p＞0）的焦点为F，准线为直线l，点A、B在直线l上，点M为抛物线E第一象限上的点，△ABM是边长为的等边三角形，直线MF的倾斜角为60°．
（1）求抛物线E的方程；
（2）如图，直线m过点F交抛物线E于C、D两点，Q（2，0），直线CQ、DQ分别交抛物线E于G、H两点，设直线CD、GH的斜率分别为k1、k2 ，求的值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图，在平面直角坐标系中，点F（﹣1，0），过直线l：x=﹣2右侧的动点P作PA⊥l于点A，∠APF的平分线交x轴于点B，|PA|= |BF|．

（1）求动点P的轨迹C的方程；
（2）过点F的直线q交曲线C于M，N，试问：x轴正半轴上是否存在点E，直线EM，EN分别交直线l于R，S两点，使∠RFS为直角？若存在，求出点E的坐标，若不存在，请说明理由．