
【题目】执行如图所示的程序框图,则“3<m<5”是“输出i的值为5”的( ) 
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
【答案】B
【解析】解:第一次执行循环体后,S=2,i=2,应该不满足退出循环的条件;
第二次执行循环体后,S=6,i=3,应该不满足退出循环的条件;
第三次执行循环体后,S=13,i=4,应该不满足退出循环的条件;
第四次执行循环体后,S=23,i=5,应该满足退出循环的条件;
故 ![]() ,解得:
,解得: ![]() ,
,
故“3<m<5”是“输出i的值为5”的必要不充分条件,
故选:B
【考点精析】根据题目的已知条件,利用程序框图的相关知识可以得到问题的答案,需要掌握程序框图又称流程图,是一种用规定的图形、指向线及文字说明来准确、直观地表示算法的图形;一个程序框图包括以下几部分:表示相应操作的程序框;带箭头的流程线;程序框外必要文字说明.


科目:高中数学 来源: 题型:
【题目】高二年级有甲、乙、丙三个班参加社会实践活动,高二年级老师要分到各个班级带队,其中男女老师各一半,每次任选两个老师,将其中一个老师分到甲班,如果这个老师是男老师,就将另一个老师分到乙班,否则就分到丙班,重复上述过程,直到所有老师都分到班级,则
A. 乙班女老师不多于丙班女老师 B. 乙班男老师不多于丙班男老师
C. 乙班男老师与丙班女老师一样多 D. 乙班女老师与丙班男老师一样多
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PA⊥平面ABCD,PA=AB=AD=2,四边形ABCD满足AB⊥AD,BC∥AD且BC=4,点M为PC的中点,点E为BC边上的点,且 ![]() =λ.
=λ. 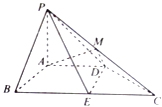
(1)求证:平面ADM⊥平面PBC;
(2)是否存在实数λ,使得二面角P﹣DE﹣B的余弦值为 ![]() ?若存在,求出实数λ的值,若不存在,请说明理由.
?若存在,求出实数λ的值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=![]() 满足:对任意的实数x1≠x2,都有(x1-x2)[f(x1)-f(x2)]>0成立,则实数a的取值范围是( )
满足:对任意的实数x1≠x2,都有(x1-x2)[f(x1)-f(x2)]>0成立,则实数a的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设全集U=R,集合A={x|2x-1≥1},B={x|x2-4x-5<0}.
(Ⅰ)求A∩B,(UA)∪(UB);
(Ⅱ)设集合C={x|m+1<x<2m-1},若B∩C=C,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=a2x+2ax-1(a>1,且a为常数)在区间[-1,1]上的最大值为14.
(1)求f(x)的表达式;
(2)求满足f(x)=7时x的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】正方形![]() 的棱长为1,点
的棱长为1,点![]() 分别是棱
分别是棱![]() 的中点.
的中点.
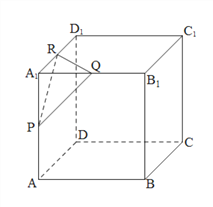
(Ⅰ)求二面角![]() 的余弦值;
的余弦值;
(Ⅱ)以![]() 为底面作正三棱柱,若此三棱柱另一底面三个顶点也都在该正方体的表面上,求这个正三棱柱的高.
为底面作正三棱柱,若此三棱柱另一底面三个顶点也都在该正方体的表面上,求这个正三棱柱的高.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知极点与直角坐标系的原点重合,极轴与x轴的正半轴重合,圆C的极坐标方程是ρ=asinθ,直线l的参数方程是  (t为参数)
(t为参数)
(1)若a=2,直线l与x轴的交点是M,N是圆C上一动点,求|MN|的最大值;
(2)直线l被圆C截得的弦长等于圆C的半径的 ![]() 倍,求a的值.
倍,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂计划出售一种产品,经销人员并不是根据生产成本来确定这种产品的价格,而是通过对经营产品的零售商对于不同的价格情况下他们会进多少货进行调查,通过调查确定了关系式P=-750x+15000,其中P为零售商进货的数量(单位:件),x为零售商支付的每件产品价格(单位:元).现估计生产这种产品每件的材料和劳动生产费用为4元,并且工厂生产这种产品的总固定成本为7000元(固定成本是除材料和劳动费用以外的其他费用),为获得最大利润,工厂应对零售商每件收取多少元?并求此时的最大利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com