
【题目】当前全世界人民越来越关注环境保护问题,某地某监测站点于2018年8月起连续n天监测空气质量指数(AQI),数据统计如下表:
空气质量指数(μg/m3) | [0,50] | (50,100] | (100,150] | (150,200] | (200,250] |
空气质量等级 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 |
天数 | 20 | 40 | m | 10 | 5 |
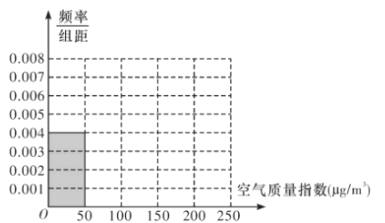
(1)根据所给统计表和频率分布直方图中的信息求出n,m的值,并完成频率分布直方图;
(2)由频率分布直方图,求该组数据的平均数与中位数;
(3)在空气质量指数分别为[0,50]和(50,100]的监测数据中,用分层抽样的方法抽取6天,从中任意选取2天,求事件A“两天空气质量等级都为良”发生的概率。
【答案】(1)见解析(2)平均数为95,中位数为![]() (3)
(3)![]()
【解析】
(1)由频率分布表求出n,m,由此能完成频率分布直方图.
(2)由频率分布直方图能求出该组数据的平均数和中位数.
(3)由题意知在空气质量指数为[0,50]和(50,100]的监测天数中分别抽取2天和4天.在所抽取的6天中,将空气质量指数为[0,50]的2天记为x,y,空气质量指数为(50,100]的4天记为a,b,c,d,从中任取2天,利用列举法能求出事件A“两天空气质量等级都为良”发生的概率.
(1).∵![]() ,.∴n=100.
,.∴n=100.
∴20+40+m+10+5=100.∴m=25
![]() ;
;![]() ;
;![]() ;
;![]() ,
,
由此完成频率分布直方图如图.
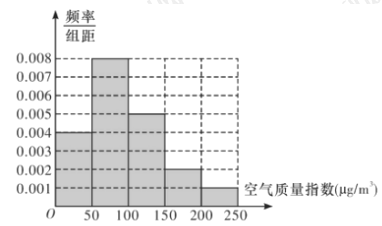
(2).由频率分布直方图得该组数据的平均数为25×0.004×50+75×0.008×50+125×0.005×50+175×0.002×50+225×0.001×50=95,
∵[0,50]的频率为0.004×50=0.2,(50,100]的频率为0.008×50=0.4,
∴中位数为![]()
(3).由题意知在空气质量指数为[0,50]和(50,100]的监测天数中分别抽取2天和4天.
在所抽取的6天中,将空气质量指数为[0,50]的2天记为x,y,
空气质量指数为(50,100]的4天记为a,b,c,d,
则从中任取2天的基本事件为(x,y),(x,a),(x,b),(x,c),(x,d),(y,a),(y,b),(y,c),(y,d),(a,b),(a,c),(a,d),(b,c),(b,d),(c,d),共计15个,
其中事件A“两天空气质量等级为良”包含的基本事件有6个,∴![]() .
.


科目:高中数学 来源: 题型:
【题目】十三届全国人大二次会议于2019年3月5日在京召开.为了了解某校大学生对两会的关注程度,学校媒体在开幕后的第二天,从学生中随机抽取了180人,对是否收看2019年两会开幕会情况进行了问卷调查,统计数据得到列联表如下:
收看 | 没收看 | 合计 | |
男生 | 40 | ||
女生 | 30 | 60 | |
合计 |
(1)请完成列联表;
(2)根据上表说明,能否有99%的把握认为该校大学生收看开幕会与性别有关?(结果精确到0.001)
附: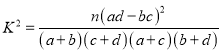 ,其中
,其中![]() .
.
| 0.10 | 0.05 | 0.025 | 0.01 | 0.005 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的内角A,B,C的对边分别为a,b,c,已知△ABC的面积为![]()
(1)求sinBsinC;
(2)若6cosBcosC=1,a=3,求△ABC的周长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场举行优惠促销活动,顾客仅可以从以下两种优惠方案中选择一种,
方案一:每满200元减50元;
方案二:每满200元可抽奖一次.具体规则是依次从装有3个红球、l个白球的甲箱,装有2个红球、2个白球的乙箱,以及装有1个红球、3个白球的丙箱中各随机摸出1个球,所得结果和享受的优惠如下表:(注:所有小球仅颜色有区别)
红球个数 | 3 | 2 | 1 | 0 |
实际付款 | 半价 | 7折 | 8折 | 原价 |
(1)若两个顾客都选择方案二,各抽奖一次,求至少一个人获得半价优惠的概率;
(2)若某顾客购物金额为320元,用所学概率知识比较哪一种方案更划算?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4坐标系与参数方程选讲
在直角坐标系中,以原点为极点,![]() 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线![]() ,过点
,过点![]() 的直线
的直线![]() 的参数方程为
的参数方程为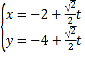 (
(![]() 为参数),直线
为参数),直线![]() 与曲线
与曲线![]() 分别交于
分别交于![]() ,
,![]() 两点.
两点.
(1)写出曲线![]() 的平面直角坐标方程和直线
的平面直角坐标方程和直线![]() 的普通方程:
的普通方程:
(2)若![]() 成等比数列,求实数
成等比数列,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(Ⅰ)若函数f(x)的最小值为8,求实数a的值;
(Ⅱ)若函数g(x)=|f(x)|+f(x)﹣16有4个零点,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱锥![]() (如图一)的平面展开图(如图二)中,四边形
(如图一)的平面展开图(如图二)中,四边形![]() 为边长等于
为边长等于![]() 的正方形,
的正方形,![]() 和
和![]() 均为正三角形,在三棱锥
均为正三角形,在三棱锥![]() 中:
中:
(I)证明:平面![]() 平面
平面![]() ;
;
(Ⅱ)若点![]() 在棱
在棱![]() 上运动,当直线
上运动,当直线![]() 与平面
与平面![]() 所成的角最大时,求二面角
所成的角最大时,求二面角![]() 的余弦值.
的余弦值.
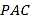
图一
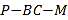
图二
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com