
【题目】已知函数![]() .
.
(Ⅰ)当![]() 时,求函数
时,求函数![]() 的极小值;
的极小值;
(Ⅱ)设定义在![]() 上的函数
上的函数![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() :
:![]() ,当
,当![]() 时,若
时,若![]() 在
在![]() 内恒成立,则称
内恒成立,则称![]() 为函数
为函数![]() 的“转点”.当
的“转点”.当![]() 时,试问函数
时,试问函数![]() 是否存在“转点”?若存在,求出转点的横坐标;若不存在,请说明理由.
是否存在“转点”?若存在,求出转点的横坐标;若不存在,请说明理由.
【答案】(1)当![]() 时,函数
时,函数![]() 取到极大值为
取到极大值为![]() ,当
,当![]() 时,函数
时,函数![]() 取到极小值为-2.
取到极小值为-2.
(2)函数![]() 存在“转点”,且2是“转点”的横坐标.
存在“转点”,且2是“转点”的横坐标.
【解析】试题分析:(1)先求导,令导数大于0得增区间,令导数小于0得减区间,根据单调性求最值. (2)求导,根据导数的几何意义得点![]() 处切线的斜率,根据点斜式得切线方程,从而可得
处切线的斜率,根据点斜式得切线方程,从而可得![]() 的解析式,因为
的解析式,因为![]() 是函数
是函数![]() 图像和切线的交点,则
图像和切线的交点,则![]() .将函数
.将函数![]() 求导,用导数求其单调性,讨论
求导,用导数求其单调性,讨论![]() 的取值范围判断
的取值范围判断![]() 是否恒成立.
是否恒成立.
试题解析:解:(1)当![]() 时,
时,![]()
当![]() ,当
,当![]() ,
,
所以函数![]() 在
在![]() 和
和![]() 单调递增,在
单调递增,在![]() 单调递减,
单调递减,
所以当![]() 时,函数
时,函数![]() 取到极大值为
取到极大值为![]() ,
,
当![]() 时,函数
时,函数![]() 取到极小值为-2. 6分
取到极小值为-2. 6分
(2)当![]() 时,函数
时,函数![]() 在其图像上一点
在其图像上一点![]() 处的切线方程为
处的切线方程为
![]() 8分
8分
设![]()
且![]()
![]()
当![]() 时,
时,![]() 在
在![]() 上单调递减,
上单调递减,
所以当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() 在
在![]() 上单调递减,
上单调递减,
所以当![]() 时,
时,![]() ;
;
所以![]() 在
在![]() 不存在“转点” 11分
不存在“转点” 11分
当![]() 时,
时,![]() ,即
,即![]() 在
在![]() 上是增函数.
上是增函数.
当![]() 时,
时,![]() 当
当![]() 时,
时,![]() 即点
即点![]() 为“转点”.
为“转点”.
故函数![]() 存在“转点”,且2是“转点”的横坐标. 12分
存在“转点”,且2是“转点”的横坐标. 12分


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左右焦点与其短轴得一个端点是正三角形的三个顶点,点
的左右焦点与其短轴得一个端点是正三角形的三个顶点,点![]() 在椭圆
在椭圆![]() 上,直线
上,直线![]() 与椭圆交于
与椭圆交于![]() 两点,与
两点,与![]() 轴,
轴, ![]() 轴分别相交于点
轴分别相交于点![]() 合点
合点![]() ,且
,且![]() ,点
,点![]() 时点
时点![]() 关于
关于![]() 轴的对称点,
轴的对称点, ![]() 的延长线交椭圆于点
的延长线交椭圆于点![]() ,过点
,过点![]() 分别做
分别做![]() 轴的垂线,垂足分别为
轴的垂线,垂足分别为![]() .
.
(1) 求椭圆![]() 的方程;
的方程;
(2)是否存在直线![]() ,使得点
,使得点![]() 平分线段
平分线段![]() ?若存在,请求出直线
?若存在,请求出直线![]() 的方程;若不存在,请说明理由。
的方程;若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】拖延症总是表现在各种小事上,但日积月累,特别影响个人发展.某校的一个社会实践调查小组,在对该校学生进行“是否有明显拖延症”的调查中,随机发放了110份问卷.对收回的100份有效问卷进行统计,得到如下![]() 列联表:
列联表:
有明显拖延症 | 无明显拖延症 | 合计 | |
男 | 35 | 25 | 60 |
女 | 30 | 10 | 40 |
合计 | 65 | 35 | 100 |
(Ⅰ)按女生是否有明显拖延症进行分层,已经从40份女生问卷中抽取了8份问卷,现从这8份问卷中再随机抽取3份,并记其中无明显拖延症的问卷的份数为![]() ,试求随机变量
,试求随机变量![]() 的分布列和数学期望;
的分布列和数学期望;
(Ⅱ)若在犯错误的概率不超过![]() 的前提下认为无明显拖延症与性别有关,那么根据临界值表,最精确的
的前提下认为无明显拖延症与性别有关,那么根据临界值表,最精确的![]() 的值应为多少?请说明理由.
的值应为多少?请说明理由.
附:独立性检验统计量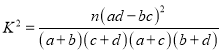 ,其中
,其中![]() .
.
独立性检验临界值表:
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司试销一种成本单价为500元的新产品,规定试销时销售单价不低于成本单价,又不高于800元.经试销调查,发现销售量y(件)与销售单价x(元)之间的关系可近似看作一次函数y=kx+b(k≠0),函数图象如图所示.

(1)根据图象,求一次函数y=kx+b(k≠0)的表达式;
(2)设公司获得的毛利润(毛利润=销售总价-成本总价)为S元.试问销售单价定为多少时,该公司可获得最大毛利润?最大毛利润是多少?此时的销售量是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是定义在
是定义在![]() 上的奇函数,且
上的奇函数,且![]() .若对任意的
.若对任意的![]() ,
, ![]() 都有
都有![]() .
.
(1)用函数单调性的定义证明: ![]() 在定义域上为增函数;
在定义域上为增函数;
(2)若![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)若不等式![]() 对所有的
对所有的![]() 和
和![]() 都恒成立,求实数
都恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com