【题目】近期“共享单车”在全国多个城市持续升温，某移动互联网机构通过对使用者的调查得出，现在市场上常见的八个品牌的“共享单车”的满意度指数如茎叶图所示：
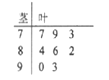
（Ⅰ）求出这组数据的平均数和中位数；
（Ⅱ）某用户从满意度指数超过80的品牌中随机选择两个品牌使用，求所选两个品牌的满意度指数均超过85的概率.
【答案】（Ⅰ）平均数
；中位数为83 （Ⅱ）概率为
【解析】【试题分析】（1）先依据题设条件中茎叶图得到中位数，再运用平均数的计算公式求出
；（2）先搞清楚满意度指数超过80的品牌有5个，进而求出任选两个有
种，再求出所选两个品牌的满意度指数均超过85的有
种，运用古典概型的计算公式从而求出满足题设条件的概率：
解：（Ⅰ）平均数
；
8个数按从小到大的顺序排列为：73,77,79,82,84,86,90,93.这组数据最中间的两个数的平均数为
，故这组数据的中位数为83.
（Ⅱ）满意度指数超过80的品牌有5个，从中任选两个有
种，其中所选两个品牌的满意度指数均超过85的有
种，故所选两个品牌的满意度指数均超过85的概率为
.
科目：高中数学 来源： 题型：
【题目】在等差数列{an}中，a2+a7=﹣23，a3+a8=﹣29．
（1）求数列{an}的通项公式；
（2）设数列{an+bn}是首项为1，公比为c的等比数列，求{bn}的前n项和Sn ．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】若二次函数f（x）=ax2+bx+c（a，b，c∈R）满足f（x+1）﹣f（x）=4x+1，且f（0）=3．
（1）求f（x）的解析式；
（2）若在区间[﹣1，1]上，不等式f（x）＞6x+m恒成立，求实数m的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】对于x∈R，[x]表示不超过x的最整数，如[1.1]=1，[﹣2.1]=﹣3．定义R上的函数f（x）=[2x]+[4x]+[8x]，若A={y|y=f（x），0≤x≤ 
}，则A中所有元素的和为（ ）
A.15
B.19
C.20
D.55
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知a∈R，函数f（x）=x|x﹣a|．
（1）当a=2时，将函数f（x）写成分段函数的形式，并作出函数的简图，写出函数y=f（x）的单调递增区间；
（2）当a＞2时，求函数y=f（x）在区间[1，2]上的最小值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在锐角△ABC中，内角A，B，C的对边分别为a，b，c，且2asinB= 
b．
（1）求角A的大小；
（2）若a=4，b+c=8，求△ABC的面积．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）+2= 
，当x∈（0，1]时，f（x）=x2 ， 若在区间（﹣1，1]内，g（x）=f（x）﹣t（x+2）有两个不同的零点，则实数t的取值范围是（ ）
A.（0， 
]
B.（0， 
]
C.[﹣ ， ]
D.[﹣ ， ]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
