
【题目】若函数![]() 的图象和直线
的图象和直线![]() 无交点,给出下列结论:
无交点,给出下列结论:
①方程![]() 一定没有实数根;
一定没有实数根;
②若![]() ,则必存在实数
,则必存在实数![]() ,使
,使![]() ;
;
③若![]() ,则不等式
,则不等式![]() 对一切实数
对一切实数![]() 都成立;
都成立;
④函数![]() 的图象与直线
的图象与直线![]() 也一定没有交点.
也一定没有交点.
其中正确的结论个数有( )
A. 1个 B. 2个 C. 3个 D. 4个
科目:高中数学 来源: 题型:
【题目】“中国式过马路”存在很大的交通安全隐患.某调查机构为了解路人对“中国式过马路”的态度是否与性别有关,从马路旁随机抽取30名路人进行了问卷调查,得到了如下列联表:
男性 | 女性 | 合计 | |
反感 | 10 | ||
不反感 | 8 | ||
合计 | 30 |
已知在这30人中随机抽取1人抽到反感“中国式过马路”的路人的概率是 ![]() .
.
(Ⅰ)请将上面的列联表补充完整(在答题卡上直接填写结果,不需要写求解过程),并据此资料分析反感“中国式过马路”与性别是否有关?
(Ⅱ)若从这30人中的女性路人中随机抽取2人参加一活动,记反感“中国式过马路”的人数为X,求X的分布列和数学期望.
提示:可参考试卷第一页的公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R的函数![]() 是偶函数,且满足
是偶函数,且满足![]() 上的解析式为
上的解析式为![]() ,过点
,过点![]() 作斜率为k的直线l,若直线l与函数
作斜率为k的直线l,若直线l与函数![]() 的图象至少有4个公共点,则实数k的取值范围是
的图象至少有4个公共点,则实数k的取值范围是
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,四棱锥 ![]() 的底面为直角梯形,
的底面为直角梯形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 底面
底面 ![]() ,
, ![]() 为
为 ![]() 的中点.
的中点.
(Ⅰ)求证:平面 ![]() 平面
平面 ![]()
(Ⅱ)求直线 ![]() 与平面
与平面 ![]() 所成的角的正弦值.
所成的角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图(甲),在直角梯形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,且
,且![]() ,
, ![]() ,
, ![]() 、
、![]() 、
、![]() 分别为
分别为![]() 、
、![]() 、
、![]() 的中点,现将
的中点,现将![]() 沿
沿![]() 折起,使平面
折起,使平面![]() 平面
平面![]() ,如图(乙).
,如图(乙).
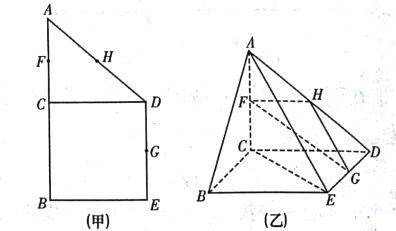
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,半圆AOB是某市休闲广场的平面示意图,半径OA的长为10,管理部门在A,B两处各安装好一个光源,其相应的光强度分别为4和9,根据光学原理,地面上某处照度y与光强度I成正比,与光源距离x的平方成反比,即y= ![]() (k为比例系数),经测量,在弧AB的中心C处的照度为130.(C处的照度为A,B两处光源的照度之和)
(k为比例系数),经测量,在弧AB的中心C处的照度为130.(C处的照度为A,B两处光源的照度之和) 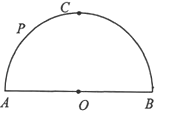
(1)求比例系数k的值;
(2)现在管理部门计划在半圆弧AB上,照度最小处增设一个光源P,试问新增光源P安装在什么位置?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx.
(1)设h(x)为偶函数,当x<0时,h(x)=f(﹣x)+2x,求曲线y=h(x)在点(1,﹣2)处的切线方程;
(2)设g(x)=f(x)﹣mx,求函数g(x)的极值;
(3)若存在x0>1,当x∈(1,x0)时,恒有f(x)> ![]() 成立,求实数k的取值范围.
成立,求实数k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com