若函数
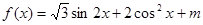
在区间
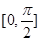
上的最小值为3,
(1)求常数
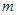
的值;
(2)求此函数当
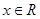
时的最大值和最小值,并求相应的
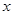
的取值集合。
(1)因为函数
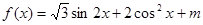
可化为

,即

,当
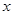

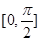
时,
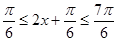
,所以

,

,

-----6分
(2)因为

,所以当
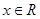
时,

,即

时,

,

,即

时,

练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:解答题
已知向量


,

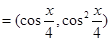
,函数


.
(1)若

,求

的值;
(2)在锐角△ABC中,角A,B,C的对边分别是

,且满足

,求

的取值范围.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知函数
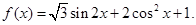
(Ⅰ)求函数

的单调递增区间;
(Ⅱ)设

的内角

对边分别为

,且

,

,
若

,求

的值.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知
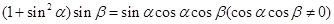
,设
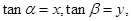
记
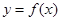
.
(Ⅰ)
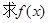
的解析表达式;
(Ⅱ)若
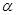
角是一个三角形的最小内角,试求函数
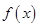
的值域
查看答案和解析>>

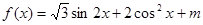 在区间
在区间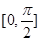 上的最小值为3,
上的最小值为3,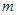 的值;
的值;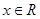 时的最大值和最小值,并求相应的
时的最大值和最小值,并求相应的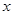 的取值集合。
的取值集合。