已知二次函数f(x)=x2+(a+2)x+b满足f(-1)=-2.
(1)若方程f(x)=2x有唯一解,求实数a,b的值;
(2)当x∈[-2,2]时,函数f(x)在顶点取得最小值,求实数a的取值范围.
解:由f(-1)=-2得:1-a-2+b=-2,即a-b=1①,
(1)把f(x)的解析式代入f(x)=2x中,得到x
2+ax+b=0,
因为方程由唯一的解,所以△=a
2-4b=0②,
由①得:a=b+1,代入②得:(b-1)
2=0,解得b=1,把b=2代入①解得:a=2;
(2)因为二次函数f(x)=x
2+(a+2)x+b为开口向上的抛物线,且当x∈[-2,2]时,函数f(x)在顶点取得最小值,
所以对称轴x=-
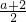
∈[-2,2],即
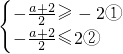
,
由①解得:a≤2;由②解得a≥-6,所以不等式组的解集为-6≤x≤2.
故a的取值范围是-6≤x≤2.
分析:先根据f(-1)=2,把x=-1代入f(x)的解析式中让其值等于-2得到关于a与b的关系式,记作①,
(1)把f(x)的解析式代入到f(x)=2x中化为一般形式,由方程有唯一的解得到△=0,即可列出关于a与b的关系式,记作②,联立①②即可求出a与b的值;
(2)由函数解析式可知,此二次函数为开口向上的抛物线,又当x∈[-2,2]时,函数f(x)在顶点取得最小值,得到其对称轴在区间内,根据f(x)解析式表示出对称轴,让对称轴大于等于-2和小于等于2列出关于a的不等式组,求出不等式组的解集即可得到a的取值范围.
点评:此题考查学生会利用根的判别式判断方程解的情况,掌握二次函数的图象与性质,是一道综合题.

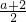 ∈[-2,2],即
∈[-2,2],即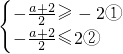 ,
,

 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案