
【题目】已知函数![]() .
.
(1)若![]() 是偶函数,求
是偶函数,求![]() 的值;
的值;
(2)设函数![]() ,当
,当![]() 时,
时,![]() 有且只有一个实数根,求
有且只有一个实数根,求![]() 的取值范围;
的取值范围;
(3)若关于![]() 的方程
的方程![]() 在区间
在区间![]() 上有两个不相等的实数根
上有两个不相等的实数根![]() ,
,![]() ,证明:
,证明:![]() .
.
科目:高中数学 来源: 题型:
【题目】一种排卡游戏规则如下:将写有![]() 的九张卡片随机地排成一行,第一张卡片:左起)上的标数为
的九张卡片随机地排成一行,第一张卡片:左起)上的标数为![]() ,则将前
,则将前![]() 张卡片逆序排过来称为一次操作,无法操作时(即第一张卡片上的标数“1”)游戏停止.若一个排列无法操作,且恰由唯一的另一个排列经过一次操作得到,则此排列称为“二次终止排列”.在所有可能的排列中,求二次终止排列出现的概率.
张卡片逆序排过来称为一次操作,无法操作时(即第一张卡片上的标数“1”)游戏停止.若一个排列无法操作,且恰由唯一的另一个排列经过一次操作得到,则此排列称为“二次终止排列”.在所有可能的排列中,求二次终止排列出现的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着西部大开发的深入,西南地区的大学越来越受到广大考生的青睐,下表是西南地区某大学近五年的录取平均分高于省一本线分值对比表:
年份 | 2015 | 2016 | 2017 | 2018 | 2019 |
年份代码 | 1 | 2 | 3 | 4 | 5 |
录取平均分高于省一本线分值 | 28 | 34 | 41 | 47 | 50 |
(1)根据上表数据可知,![]() 与
与![]() 之间存在线性相关关系,求
之间存在线性相关关系,求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)假设2020年该省一本线为520分,利用(1)中求出的回归方程预测2020年该大学录取平均分.
参考公式: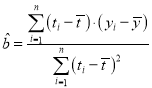 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是2020年2月1日到2月20日,某地区新型冠状病毒疫情新增数据的走势图.

(Ⅰ)从这20天中任选1天,求新增确诊和新增疑似的人数都超过100的概率;
(Ⅱ)从新增确诊的人数超过100的日期中任选两天,用X表示新增确诊的人数超过140的天数,求X的分布列和数学期望;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,过点![]() 的直线
的直线![]() 的参数方程为:
的参数方程为: (
(![]() 为参数), 以原点为极点,
为参数), 以原点为极点,![]() 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线![]()
![]() ,直线
,直线![]() 与曲线
与曲线![]() 分别交于
分别交于![]() 两点.
两点.
(1)写出曲线![]() 和
和![]() 的普通方程;
的普通方程;
(2)若![]() 成等比数列,求
成等比数列,求![]() 值.
值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某造船公司年造船量是20艘,已知造船![]() 艘的产值函数为
艘的产值函数为![]() (单位:万元),成本函数为
(单位:万元),成本函数为![]() (单位:万元),又在经济学中,函数
(单位:万元),又在经济学中,函数![]() 的边际函数
的边际函数![]() 定义为
定义为![]() .
.
(1)求利润函数![]() 及边际利润函数
及边际利润函数![]() .(提示:利润=产值-成本)
.(提示:利润=产值-成本)
(2)问年造船量安排多少艘时,可使公司造船的年利润最大?
(3)求边际利润函数![]() 的单调递减区间,并说明单调递减在本题中的实际意义是什么?
的单调递减区间,并说明单调递减在本题中的实际意义是什么?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于两个定义域相同的函数![]() 、
、![]() ,若存在实数
,若存在实数![]() ,
,![]() ,使
,使![]() 则称函数
则称函数![]() 是由“基函数
是由“基函数![]() ”生成的.
”生成的.
(1)若![]() 和
和![]() 生成一个偶函数
生成一个偶函数![]() ,求
,求![]() 的值;
的值;
(2)若![]() 是由
是由![]() 和
和![]() 生成,其中
生成,其中![]() ,
,![]() .且
.且![]() 求
求![]() 的取值范围;
的取值范围;
(3)利用“基函数![]() ,
,![]() ”生成一个函数
”生成一个函数![]() ,使得
,使得![]() 满足:
满足:
①是偶函数,②有最小值![]() ,求
,求![]() 的解析式.
的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com