
【题目】设函数![]() .
.
(1)求f(x)的单调区间;
(2)若当![]() 时,不等式f (x)<m恒成立,求实数m的取值范围;
时,不等式f (x)<m恒成立,求实数m的取值范围;
(3)若关于x的方程f(x)=x2+x+a在区间[0,2]上恰好有两个相异的实根,求实数a的取值范围.
【答案】(1)递增区间是(-2,-1),(0,+∞),递减区间是![]() .
.
(2)m>e2﹣2.(3)2﹣2ln2<a≤3﹣2ln3.
【解析】
(1)已知f(x)=(1+x)2﹣ln(1+x)2求出函数的导数f′(x),然后令f′(x)=0,解出函数的极值点,最后根据导数判断函数的单调性,从而求解;
(2)由题意当![]() 时,不等式f (x)<m恒成立,只要求出f(x)的最大值小于m就可以了,从而求出实数m的取值范围;
时,不等式f (x)<m恒成立,只要求出f(x)的最大值小于m就可以了,从而求出实数m的取值范围;
(3)将原式变形转化得方程g(x)=x﹣a+1﹣2ln(1+x)=0在区间[0,2]上恰好有两个相异的实根,结合函数的单调性及图象,得到 ,从而求出实数a的取值范围.
,从而求出实数a的取值范围.
(1)函数的定义域为![]() .
.
∵![]() ,
,
由f′(x)>0,得x>0或-2<x<-1;由f′(x)<0,得﹣1<x<0或x<-2.
∴f(x)的递增区间是(-2,-1),(0,+∞),递减区间是![]() .
.
(2)∵由![]() ,得x=0,x=﹣2(舍去)
,得x=0,x=﹣2(舍去)
由(1)知f(x)在![]() 上递减,在[0,e﹣1]上递增.
上递减,在[0,e﹣1]上递增.
又![]() ,f(e﹣1)=e2﹣2,且
,f(e﹣1)=e2﹣2,且![]() .
.
∴当![]() 时,f(x)的最大值为e2﹣2.
时,f(x)的最大值为e2﹣2.
故当m>e2﹣2时,不等式f(x)<m恒成立.
(3)方程f(x)=x2+x+a,x﹣a+1﹣2ln(1+x)=0.
记g(x)=x﹣a+1﹣2ln(1+x),
∵![]() ,
,
由g′(x)>0,得x>1或x<﹣1(舍去).由g′(x)<0,得﹣1<x<1.
∴g(x)在[0,1]上递减,在[1,2]上递增.
为使方程f(x)=x2+x+a在区间[0,2]上恰好有两个相异的实根,
只须g(x)=0在[0,1]和(1,2]上各有一个实数根,于是有
∵2﹣2ln2<3﹣2ln3,
∴实数a的取值范围是2﹣2ln2<a≤3﹣2ln3.


科目:高中数学 来源: 题型:
【题目】某校高一某班的一次数学测试成绩的茎叶图和频率分布直方图因事故都受到不同程度的损坏,但可见部分如下,据此解答如下问题:
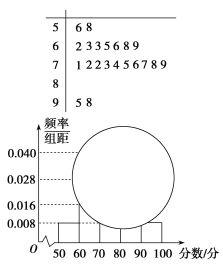
(1)求分数在[50,60)的频率及全班人数;
(2)求分数在[80,90)的频数,并计算频率分布直方图中[80,90)间的矩形的高;
(3)若规定:90分(包含90分)以上为优秀,现从分数在80分(包含80分)以上的试卷中任取两份分析学生失分情况,求在抽取的试卷中至少有一份优秀的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,过抛物线![]() 上的一点
上的一点![]() 作抛物线的切线,分别交x轴于点D交y轴于点B,点Q在抛物线上,点E,F分别在线段AQ,BQ上,且满足
作抛物线的切线,分别交x轴于点D交y轴于点B,点Q在抛物线上,点E,F分别在线段AQ,BQ上,且满足![]() ,
,![]() ,线段QD与
,线段QD与![]() 交于点P.
交于点P.

(1)当点P在抛物线C上,且![]() 时,求直线
时,求直线![]() 的方程;
的方程;
(2)当![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】苹果可按果径![]() (最大横切面直径,单位:
(最大横切面直径,单位:![]() .)分为五个等级:
.)分为五个等级:![]() 时为1级,
时为1级,![]() 时为2级,
时为2级,![]() 时为3级,
时为3级,![]() 时为4级,
时为4级,![]() 时为5级.不同果径的苹果,按照不同外观指标又分为特级果、一级果、二级果.某果园采摘苹果10000个,果径
时为5级.不同果径的苹果,按照不同外观指标又分为特级果、一级果、二级果.某果园采摘苹果10000个,果径![]() 均在
均在![]() 内,从中随机抽取2000个苹果进行统计分析,得到如图1所示的频率分布直方图,图2为抽取的样本中果径在80以上的苹果的等级分布统计图.
内,从中随机抽取2000个苹果进行统计分析,得到如图1所示的频率分布直方图,图2为抽取的样本中果径在80以上的苹果的等级分布统计图.

(1)假设![]() 服从正态分布
服从正态分布![]() ,其中
,其中![]() 的近似值为果径的样本平均数
的近似值为果径的样本平均数![]() (同一组数据用该区间的中点值代替),
(同一组数据用该区间的中点值代替),![]() ,试估计采摘的10000个苹果中,果径
,试估计采摘的10000个苹果中,果径![]() 位于区间
位于区间![]() 的苹果个数;
的苹果个数;
(2)已知该果园今年共收获果径在80以上的苹果![]() ,且售价为特级果12元
,且售价为特级果12元![]() ,一级果10元
,一级果10元![]() ,二级果9元
,二级果9元![]() .设该果园售出这
.设该果园售出这![]() 苹果的收入为
苹果的收入为![]() ,以频率估计概率,求
,以频率估计概率,求![]() 的数学期望.
的数学期望.
附:若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则
![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市![]() 户居民的月平均用电量(单位:度),以
户居民的月平均用电量(单位:度),以![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分组的频率分布直方图如图.
分组的频率分布直方图如图.

(1)求直方图中![]() 的值;
的值;
(2)求月平均用电量的众数和中位数;
(3)在月平均用电量为![]() ,
,![]() ,
,![]() ,
,![]() 的四组用户中,用分层抽样的方法抽取
的四组用户中,用分层抽样的方法抽取![]() 户居民,则月平均用电量在
户居民,则月平均用电量在![]() 的用户中应抽取多少户?
的用户中应抽取多少户?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】阿波罗尼斯(约公元前![]() 年)证明过这样一个命题:平面内到两定点距离之比为常数
年)证明过这样一个命题:平面内到两定点距离之比为常数![]() 的点的轨迹是圆,后人将这个圆称为阿波罗尼斯圆.若平面内两定点
的点的轨迹是圆,后人将这个圆称为阿波罗尼斯圆.若平面内两定点![]() 、
、![]() 间的距离为
间的距离为![]() ,动点
,动点![]() 满足
满足![]() ,则
,则![]() 的最小值为( )
的最小值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com