对于数列{an},从第二项起,每一项与它前一项的差依次组成等比数列,称该等比数列为数列{an}的“差等比数列”,记为数列{bn}.设数列{bn}的首项b1=2,公比为q(q为常数).
(I)若q=2,写出一个数列{an}的前4项;
(II)a1与q满足什么条件,数列{an}是等比数列,并证明你的结论;
(III)若a1=1,数列{an+cn}是公差为q的等差数列,且c1=q,求数列{cn}的通项公式;并证明当1<q<2时,c5<-2q2.
【答案】
分析:(Ⅰ)根据数列{b
n}是等比数列,且b
1=2,q=2,可得b
2=4,b
3=8,由此可求个数列{a
n}的前4项;
(Ⅱ)先确定a
2=a
1+2,a
3=a
1+2+2q,根据数列{a
n}是等比数列,即可求出公比;
(Ⅲ)先确定c
n-c
n-1=q-2q
n-2,再利用叠加法,即可求数列{c
n}的通项公式,从而可证明1<q<2时,c
5<-2q
2.
解答:解:(Ⅰ)因为数列{b
n}是等比数列,且b
1=2,q=2,所以b
2=4,b
3=8,
所以a
1=1,a
2=3,a
3=1,a
15=15.(写出满足条件的一组即可)…(2分)
(Ⅱ)因为数列{b
n}是等比数列,首项b
1=2,公比为q,,所以b
2=2q,b
3=2q
2,
所以a
2=a
1+2,a
3=a
1+2+2q.
因为数列{a
n}是等比数列,
所以

,即(a
1+2)
2=a
1×(a
1+2+2q)
所以
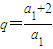
.
所以当
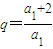
时,数列{a
n}是等比数列.…(5分)
(Ⅲ)因为{a
n+c
n}是公差为q的等差数列,所以(a
n+c
n)-(a
n-1+c
n-1)=q
∵a
n-a
n-1=2q
n-2,
∴c
n-c
n-1=q-2q
n-2,
∴c
n=c
1+(c
2-c
1)+…+(c
n-c
n-1)=nq-2(q
n-2+2q
n-3+…+q+1)=nq-
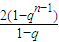
∴c
5=5q-
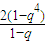
=-2q
3-2q
2+3q-2
∴c
5-(-2q
2)=2q(1-q
2)+(q-2).
∵1<q<2,∴1-q
2<0,q-2<0.
∴c
5-(-2q
2)<0
∴c
5<-2q
2. …(13分)
点评:本题考查新定义,考查等比数列的证明,考查叠加法求数列的和,正确理解新定义是关键.

 ,即(a1+2)2=a1×(a1+2+2q)
,即(a1+2)2=a1×(a1+2+2q)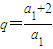 .
.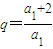 时,数列{an}是等比数列.…(5分)
时,数列{an}是等比数列.…(5分)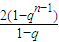
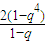 =-2q3-2q2+3q-2
=-2q3-2q2+3q-2

 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案