
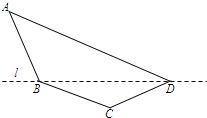
 (2012•南京二模)某单位设计一个展览沙盘,现欲在沙盘平面内,布设一个对角线在l上的四边形电气线路,如图所示.为充分利用现有材料,边BC,CD用一根5米长的材料弯折而成,边BA,AD用一根9米长的材料弯折而成,要求∠A和∠C互补,且AB=BC.
(2012•南京二模)某单位设计一个展览沙盘,现欲在沙盘平面内,布设一个对角线在l上的四边形电气线路,如图所示.为充分利用现有材料,边BC,CD用一根5米长的材料弯折而成,边BA,AD用一根9米长的材料弯折而成,要求∠A和∠C互补,且AB=BC.| 1 |
| 2 |
| (x2-4)(x2-14x+49) |
| 2 |
| x |
| 2 |
| x |
| 2 |
| x |
| 1 |
| 2 |
| 1 |
| 2 |
| 1-cos2A |
| (x2-4)(x2-14x+49) |
| 1 |
| 2 |
| 108 |
| 3 |
| 3 |


科目:高中数学 来源: 题型:
| 1 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| b |
| a |
| b |
| 13 |
| 6 |
| a |
| b |
| π |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•南京二模)一块边长为10cm的正方形铁片按如图所示的阴影部分裁下,然后用余下的四个全等的等腰三角形作侧面,以它们的公共顶点p为顶点,加工成一个如图所示的正四棱锥形容器.当x=6cm时,该容器的容积为
(2012•南京二模)一块边长为10cm的正方形铁片按如图所示的阴影部分裁下,然后用余下的四个全等的等腰三角形作侧面,以它们的公共顶点p为顶点,加工成一个如图所示的正四棱锥形容器.当x=6cm时,该容器的容积为查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com