
-
|
| π |
| 2 |
| π |
| 2 |
-
|
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:
| ∫ | 1 0 |
| ∫ | 1 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:
设y=f(x)为区间[0,1]上的连续函数,且恒有0≤f(x)≤1,可以用随机模拟方法近似计算积分![]() dx.先产生两组(每组N个)区间[0,1]上的均匀随机数x1,x2,…,xN和y1,y2,…,yN,由此得到N个点(xi,yi)(i=1,2,…,N),再数出其中满足yi
dx.先产生两组(每组N个)区间[0,1]上的均匀随机数x1,x2,…,xN和y1,y2,…,yN,由此得到N个点(xi,yi)(i=1,2,…,N),再数出其中满足yi![]() ≤f(xi)(i=1,2,…,N)的点的个数N1,那么由随机模拟方法可得积分
≤f(xi)(i=1,2,…,N)的点的个数N1,那么由随机模拟方法可得积分![]() dx的近似值为 .
dx的近似值为 .
查看答案和解析>>
科目:高中数学 来源:辽宁省10-11学年高二下学期期末考试数学(理) 题型:填空题
设 为区间
为区间 上的连续函数,且恒有
上的连续函数,且恒有 ,可以用随机模拟
,可以用随机模拟
方法近似计算积分 ,先产生两组(每组
,先产生两组(每组 个)区间
个)区间 上的均匀随机数
上的均匀随机数
 和
和 ,由此得到
,由此得到 个点
个点 。再数出其中满足
。再数出其中满足
 的点数
的点数 ,那么由随机模拟方法计算积分
,那么由随机模拟方法计算积分 的近似值为__
的近似值为__
查看答案和解析>>
科目:高中数学 来源:2010-2011年辽宁省高二下学期期末考试数学理科 题型:填空题
设 为区间
为区间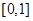 上的连续函数,且恒有
上的连续函数,且恒有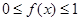 ,可以用随机模拟
,可以用随机模拟
方法近似计算积分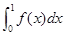 ,先产生两组(每组
,先产生两组(每组 个)区间
个)区间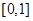 上的均匀随机数
上的均匀随机数
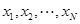 和
和 ,由此得到
,由此得到 个点
个点 。再数出其中满足
。再数出其中满足
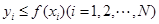 的点数
的点数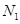 ,那么由随机模拟方法计算积分
,那么由随机模拟方法计算积分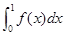 的近似值为__
的近似值为__
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com