
【题目】设![]() ,点
,点![]() 在
在![]() 轴上,点
轴上,点![]() 在
在![]() 轴上,且
轴上,且![]() ,
,![]() .
.
(1)当点![]() 在
在![]() 轴上运动时,求点
轴上运动时,求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)设点![]() 是轨迹
是轨迹![]() 上的动点,点
上的动点,点![]() 在
在![]() 轴上,圆
轴上,圆![]() 内切于
内切于![]()
![]() ,求
,求![]()
![]() 的面积的最小值.
的面积的最小值.
科目:高中数学 来源: 题型:
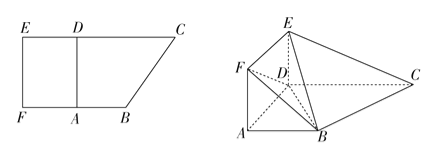
【题目】【2017银川一中模拟】如图,在直角梯形ABCD中,AB∥CD,AB⊥AD,且AB=AD=![]() CD=1.现以AD为一边向梯形外作矩形ADEF,然后沿边AD将矩形ADEF翻折,使平面ADEF与平面ABCD垂直.
CD=1.现以AD为一边向梯形外作矩形ADEF,然后沿边AD将矩形ADEF翻折,使平面ADEF与平面ABCD垂直.
(1)求证:BC⊥平面BDE;
(2)若点D到平面BEC的距离为![]() ,求三棱锥F-BDE的体积.
,求三棱锥F-BDE的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为了实现60万元的生源利润目标,准备制定一个激励招生人员的奖励方案:在生源利润达到5万元时,按生源利润进行奖励,且资金y(单位:万元)随生源利润x(单位:万元)的增加而增加,但资金总数不超过3万元,同时奖金不超过利润的20%.现有三个奖励模型:y=0.2x,y=log5x,y=1.02x,其中哪个模型符合该校的要求?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,PC⊥底面ABCD,底面ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2AD=2CD=2,E是PB的中点.
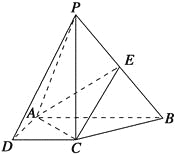
(1)求证:平面EAC⊥平面PBC;
(2)若二面角P-AC-E的余弦值为![]() ,求直线PA与平面EAC所成角的正弦值.
,求直线PA与平面EAC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex-e-x(x∈R,且e为自然对数的底数).
(1)判断函数f(x)的奇偶性与单调性.
(2)是否存在实数t,使不等式f(x-t)+f(x2-t2)≥0对一切x都成立?若存在,求出t;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一家医药研究所,从中草药中提取并合成了甲、乙两种抗“![]() 病毒”的药物,经试验,服用甲、乙两种药物痊愈的概率分别为
病毒”的药物,经试验,服用甲、乙两种药物痊愈的概率分别为![]() .现已进入药物临床试用阶段,每个试用组由4位该病毒的感染者组成,其中2人试用甲种抗病毒药物,2人试用乙种抗病毒药物,如果试用组中,甲种抗病毒药物治愈人数超过乙种抗病毒药物的治愈人数,则称该组为“甲类组”.
.现已进入药物临床试用阶段,每个试用组由4位该病毒的感染者组成,其中2人试用甲种抗病毒药物,2人试用乙种抗病毒药物,如果试用组中,甲种抗病毒药物治愈人数超过乙种抗病毒药物的治愈人数,则称该组为“甲类组”.
(1)求一个试用组为“甲类组”的概率;
(2)观察3个试用组,用![]() 表示这3个试用组中“甲类组”的个数,求
表示这3个试用组中“甲类组”的个数,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,直线l的方程为x﹣y+4=0,曲线C的参数方程为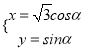 .
.
(1)已知在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,点P的极坐标为![]() ,判断点P与直线l的位置关系;
,判断点P与直线l的位置关系;
(2)设点Q是曲线C上的一个动点,求它到直线l的距离的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com