
【题目】下列四个命题中,真命题的序号有__________.(写出所有真命题的序号)①若![]() ,则“
,则“![]() ”是“
”是“![]() ”成立的充分不必要条件;②命题“
”成立的充分不必要条件;②命题“![]() 使得
使得![]() ”的否定是 “
”的否定是 “![]() 均有
均有![]() ”;③命题“若
”;③命题“若![]() ,则
,则![]() 或
或![]() ”的否命题是“若
”的否命题是“若![]() ,则
,则![]() ”;④函数
”;④函数![]() 在区间
在区间![]() 上有且仅有一个零点.
上有且仅有一个零点.
科目:高中数学 来源: 题型:
【题目】已知集合A={x|y=lg(x-![]() )},B={x|
)},B={x|![]() -cx<0,c>0},若AB,则实数c的取值范围是( )
-cx<0,c>0},若AB,则实数c的取值范围是( )
A.(0,1]B.[1,+∞)
C.(0,1)D.(1,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随机抽取了40辆汽车在经过路段上某点时的车速(km/h),现将其分成六段: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,后得到如图所示的频率分布直方图.
,后得到如图所示的频率分布直方图.
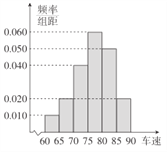
(Ⅰ)现有某汽车途经该点,则其速度低于80km/h的概率约是多少?
(Ⅱ)根据直方图可知,抽取的40辆汽车经过该点的平均速度约是多少?
(Ⅲ)在抽取的40辆且速度在![]() (km/h)内的汽车中任取2辆,求这2辆车车速都在
(km/h)内的汽车中任取2辆,求这2辆车车速都在![]() (km/h)内的概率.
(km/h)内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
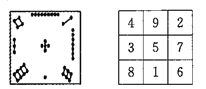
【题目】我国古代的《洛书》中记载着世界上最古老的一个幻方:如图,将1,2,…,9填入![]() 的方格内,使三行,三列和两条对角线上的三个数字之和都等于15.一般地,将连续的正整数
的方格内,使三行,三列和两条对角线上的三个数字之和都等于15.一般地,将连续的正整数![]() 填入
填入![]() 个方格中,使得每行,每列和两条对角线上的数字之和都相等,这个正方形叫做
个方格中,使得每行,每列和两条对角线上的数字之和都相等,这个正方形叫做![]() 阶幻方.记
阶幻方.记![]() 阶幻方的对角线上的数字之和为
阶幻方的对角线上的数字之和为![]() ,如图三阶幻方的
,如图三阶幻方的![]() ,那么
,那么![]() 的值为__________ .
的值为__________ .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,已知M,N分别为线段BB1,A1C的中点,MN⊥AA1,且MA1=MC.求证:
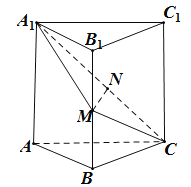
(1)MN![]() 平面ABC;
平面ABC;
(2)平面A1MC⊥平面A1ACC1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出命题:(1)对立事件一定是互斥事件.(2)若事件![]() 满足
满足![]() ,则
,则![]() 为对立事件.(3)把
为对立事件.(3)把![]() 、
、![]() 、
、![]() ,3张红桃牌随机分给甲、乙、丙三人,每人1张,事件
,3张红桃牌随机分给甲、乙、丙三人,每人1张,事件![]() :“甲得红桃
:“甲得红桃![]() ”与事件
”与事件![]() :“乙得红桃
:“乙得红桃![]() ”是对立事件.(4)一个人打靶时连续射击两次,事件“至少有一次中靶”的对立事件是两次都不中靶.其中正确的命题个数为( )
”是对立事件.(4)一个人打靶时连续射击两次,事件“至少有一次中靶”的对立事件是两次都不中靶.其中正确的命题个数为( )
A.4B.3C.2D.1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AB是圆O的直径,点C是圆O上异于A,B的点,PO垂直于圆O所在的平面,且PO=OB=1.
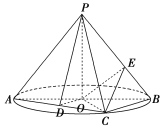
(1)若D为线段AC的中点,求证:AC⊥平面PDO;
(2)求三棱锥P-ABC体积的最大值;
(3)若![]() ,点E在线段PB上,求CE+OE的最小值.
,点E在线段PB上,求CE+OE的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 是公差为2的等差数列,且
是公差为2的等差数列,且![]() 成等比数列.数列
成等比数列.数列![]() 满足:
满足:![]() ,
,![]() .
.
(Ⅰ)求数列![]() ,
,![]() 的通项公式;
的通项公式;
(Ⅱ)设数列![]() 的前n项和为
的前n项和为![]() ,且
,且 ,若对
,若对![]() ,
,![]() 恒成立,求正整数k的值.
恒成立,求正整数k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的前n项和为Sn,等比数列{bn}的前n项和为Tn,a1=﹣1,b1=1,a2+b2=2.
(1)若a3+b3=5,求{bn}的通项公式;
(2)若T3=21,求S3.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com