
【题目】一台机器由于使用时间较长,生产的零件有一些缺损.按不同转速生产出来的零件有缺损的统计数据如下表所示:
转速x(转/秒) | 16 | 4 | 12 | 8 |
每小时生产有缺损零件数y(个) | 11 | 9 | 8 | 5 |
(1)作出散点图;
(2)如果y与x线性相关,求出回归直线方程;
(3)若实际生产中,允许每小时的产品中有缺损的零件最多为10个,那么,机器的运转速度应控制在什么范围内?
科目:高中数学 来源: 题型:
【题目】有两个分类变量x与y,其一组观测值如下面的2×2列联表所示:
y1 | y2 | |
x1 | a | 20-a |
x2 | 15-a | 30+a |
其中a,15-a均为大于5的整数,则a取何值时,在犯错误的概率不超过0.1的前提下认为x与y之间有关系?
查看答案和解析>>
科目:高中数学 来源: 题型:
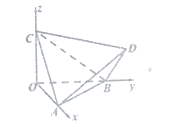
【题目】如图,正四面体![]() 的顶点
的顶点![]() 分别在两两垂直的三条射线
分别在两两垂直的三条射线![]() 上,在下列命题中,错误的是( )
上,在下列命题中,错误的是( )
A. 四面体![]() 是正三棱锥 B. 直线
是正三棱锥 B. 直线![]() 与平面
与平面![]() 相交 C. 异面直线
相交 C. 异面直线![]() 和
和![]() 所成角是
所成角是![]() D. 直线
D. 直线![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边长分别为a,b,c,B= ![]() .
.
(1)若a=3,b= ![]() ,求c的值;
,求c的值;
(2)若f(A)=sinA( ![]() cosA﹣sinA),a=
cosA﹣sinA),a= ![]() ,求f(A)的最大值及此时△ABC的外接圆半径.
,求f(A)的最大值及此时△ABC的外接圆半径.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2013·湖北高考)四名同学根据各自的样本数据研究变量x,y之间的相关关系,并求得回归直线方程,分别得到以下四个结论:
①y与x负相关且![]() =2.347x-6.423;
=2.347x-6.423;
②y与x负相关且![]() =-3.476x+5.648;
=-3.476x+5.648;
③y与x正相关且![]() =5.437x+8.493;
=5.437x+8.493;
④y与x正相关且![]() =-4.326x-4.578.
=-4.326x-4.578.
其中一定不正确的结论的序号是( )
A. ①② B. ②③ C. ③④ D. ①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】东莞市某高级中学在今年4月份安装了一批空调,关于这批空调的使用年限
![]() (单位:年,
(单位:年, ![]() )和所支出的维护费用
)和所支出的维护费用![]() (单位:万元)厂家提供的统计资料如下:
(单位:万元)厂家提供的统计资料如下:
使用年限 | 1 | 2 | 3 | 4 | 5 |
维护费用 | 6 | 7 | 7.5 | 8 | 9 |
![]() 请根据以上数据,用最小二乘法原理求出维护费用
请根据以上数据,用最小二乘法原理求出维护费用![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
![]() 若规定当维护费用
若规定当维护费用![]() 超过13.1万元时,该批空调必须报废,试根据(1)的结论求该批空调使用年限的最大值.
超过13.1万元时,该批空调必须报废,试根据(1)的结论求该批空调使用年限的最大值.
参考公式:最小二乘估计线性回归方程![]() 中系数计算公式:
中系数计算公式:
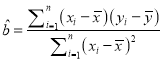 ,
, ![]() ,
, ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出40个数:1,2,4,7,11,16,…,要计算这40个数的和,如图给出了该问题的程序框图,那么框图①处和执行框②处可分别填入( )
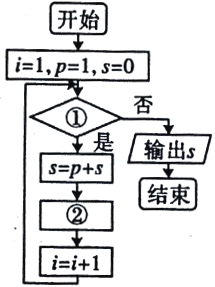
A. ![]() ;
; ![]() B.
B. ![]() ;
; ![]()
C. ![]() ;
; ![]() D.
D. ![]() ;
; ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com