
【题目】设函数![]() .
.
(1)若函数![]() 在
在![]() 上为减函数,求实数
上为减函数,求实数![]() 的最小值;
的最小值;
(2)若存在![]() ,使
,使![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)最小值为![]() ;(II)
;(II)![]()
【解析】试题分析: ![]() 在
在![]() 上为减函数,等价于
上为减函数,等价于![]() 在
在![]() 上恒成立,进而转化为
上恒成立,进而转化为![]() ,根据二次函数的性质可得
,根据二次函数的性质可得![]()
![]() 命题“若存在
命题“若存在![]() ,
,![]()
![]() ,使
,使![]() 成立”等价于
成立”等价于
“当![]() 时,有
时,有 ![]() ”, 由
”, 由![]() 易求
易求![]() ,从而问题等价于“当
,从而问题等价于“当![]() 时,有
时,有![]() ”,分
”,分![]()
![]() ,
,![]()
![]() 两种情况讨论:
两种情况讨论:
当![]() 是易求
是易求![]() ,当
,当![]() 时可求得
时可求得![]() 的值域为
的值域为![]() ,再按
,再按![]()
![]() 两种情况讨论即可
两种情况讨论即可
解析:(1)由已知得![]() ,
, ![]()
因![]() 在
在![]() 上为减函数,故
上为减函数,故![]() 在
在![]() 上恒成立。
上恒成立。
所以当![]() 时
时![]() 。
。
又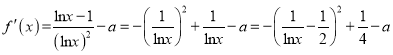 ,
,
故当![]() 时,即
时,即![]() 时,
时, ![]() .
.
所以![]() ,于是
,于是![]() ,故
,故![]() 的最小值为
的最小值为![]() .
.
(2)命题“若存在![]() ,
,![]()
![]() ,使
,使![]() 成立”等价于
成立”等价于
“当![]() 时,”
时,” ![]() ”,
”,
由(1),当![]() 时,
时, ![]() ,
, ![]()
![]() .
.
问题等价于:“当![]() 时,有
时,有![]() ”.
”.
当![]() ,由(1),
,由(1),![]() 在
在![]() 为减函数,
为减函数,
则![]() ,故
,故![]() .
.
当![]() 时,由于
时,由于![]() 在
在![]() 上的值域为
上的值域为![]()
(i)![]() ,即
,即![]() ,
, ![]() 在
在![]() 恒成立,故
恒成立,故![]() 在
在![]() 上为增函数,
上为增函数,
于是, ![]() ,矛盾。
,矛盾。
(ii)![]() ,即
,即![]() ,由
,由![]() 的单调性和值域知,
的单调性和值域知,
存在唯一![]() ,使
,使![]() ,且满足:
,且满足:
当![]() 时,
时, ![]() ,
, ![]() 为减函数;当
为减函数;当![]() 时,
时, ![]() ,
, ![]() 为增函数;
为增函数;
所以, ![]() ,
, ![]()
所以, ![]() ,与
,与![]() 矛盾。
矛盾。
综上得![]()


 名题金卷系列答案
名题金卷系列答案科目:高中数学 来源: 题型:
【题目】如图,在圆锥PO中,已知![]() ,圆O的直径
,圆O的直径![]() ,C是弧AB的中点,D为AC的中点.
,C是弧AB的中点,D为AC的中点.

(1)求异面直线PD和BC所成的角的正切值;
(2)求直线OC和平面PAC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C1的极坐标方程为ρcos θ=4.
(1)M为曲线C1上的动点,点P在线段OM上,且满足|OM|·|OP|=16,求点P的轨迹C2的直角坐标方程;
(2)设点A的极坐标为![]() ,点B在曲线C2上,求△OAB面积的最大值.
,点B在曲线C2上,求△OAB面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义在R上的偶函数,且在区间[0,+∞)上单调递增,若实数a满足f(log2a)+f( ![]() a)≤2f(1),则a的取值范围是( )
a)≤2f(1),则a的取值范围是( )
A.![]()
B.[1,2]
C.![]()
D.(0,2]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·湖南)如下图,直三棱柱ABC-A1B1C1的底面是边长为2的正三角形,E、F分别是BC、CC1的中点.
(1)证明:平面AEF⊥平面B1BCC1;
(2)若直线A1C与平面A1ABB1所成的角为45°,求三棱锥F-AEC的体积.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2x﹣ ![]() .
.
(1)若f(x)=2,求x的值;
(2)若2tf(2t)+mf(t)≥0对于t∈[1,2]恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:关于x的不等式ax>1,(a>0,a≠1)的解集是{x|x<0},命题q:函数y=lg(x2-x+a)的定义域为R,若p∨q为真,p∧q为假,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电视台“挑战主持人”节目的挑战者闯第一关需要回答三个问题,其中前两个问题回答正确各得![]() 分,回答不正确得
分,回答不正确得![]() 分,第三个问题回答正确得
分,第三个问题回答正确得![]() 分,回答不正确得
分,回答不正确得![]() 分.如果一个挑战者回答前两个问题正确的概率都是
分.如果一个挑战者回答前两个问题正确的概率都是![]() ,回答第三个问题正确的概率为
,回答第三个问题正确的概率为![]() ,且各题回答正确与否相互之间没有影响.若这位挑战者回答这三个问题总分不低于
,且各题回答正确与否相互之间没有影响.若这位挑战者回答这三个问题总分不低于![]() 分就算闯关成功.
分就算闯关成功.
(Ⅰ)求至少回答对一个问题的概率;
(Ⅱ)求这位挑战者回答这三个问题的总得分X的分布列;
(Ⅲ)求这位挑战者闯关成功的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据研究,甲磁盘受到病毒感染,感染的量y(单位: 比特数)与时间x(单位:秒)的函数关系是![]() ,乙磁盘受到病毒感染,感染的量y(单位: 比特数)与时间x(单位:秒)的函数关系是
,乙磁盘受到病毒感染,感染的量y(单位: 比特数)与时间x(单位:秒)的函数关系是![]() ,显然当
,显然当![]() 时,甲磁盘受到病毒感染增长率比乙磁盘受到病毒感染增长率大.试根据上述事实提炼一个不等式,并证明之.
时,甲磁盘受到病毒感染增长率比乙磁盘受到病毒感染增长率大.试根据上述事实提炼一个不等式,并证明之.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com