【答案】
分析:(1)利用f(x)是奇函数,可得f(-x)=-f(x),从而可求b的值,利用图象在点(e,f(e))处的切线斜率为3,可求a的值;
(2)当x>l时,设
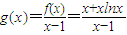
,求导函数,确定g(x)的最小值,即可求得k的最大值;
(3)要证:(nm
m)
n>(mn
n)
m,即要证nlnn+mnlnm>mlnm+mnlnn,即
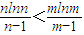
,构造函数φ(x)=
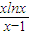
,x>1,证明φ(x)在(1,+∞)上为增函数即可.
解答:(1)解:f(x)是奇函数,所以f(-x)=-f(x),即a(-x)+(-x)ln|-x+b|=-(ax+xln|x+b|)…(2分),
所以ln|-x+b|=ln|x+b|,从而b=0…(3分),
此时f(x)=ax+xln|x|,f'(x)=a+l+ln|x|…(4分),
依题意f'(e)=a+2=3,所以a=1…(5分)
(2)解:当x>l时,设
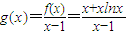
,则
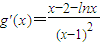
…(6分)
设h(x)=x-2-lnx,则
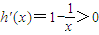
,∴h(x)在(1,+∞)上是增函数…(8分)
因为h(3)=l-ln3<0,h(4)=2-ln4>0,所以?x
∈(3,4),使h(x
)=0…(10分),
x∈(1,x
)时,h(x)<O,g'(x)<0,即g(x)在(1,x
)上为减函数;
同理g(x)在(x
,+∞)上为增函数…(12分),
从而g(x)的最小值为
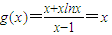
…(13分)
所以k<x
∈(3,4),k的最大值为3…(14分).
(3)证明:要证:(nm
m)
n>(mn
n)
m,即要证nlnn+mnlnm>mlnm+mnlnn…(6分),
即n(1-m)lnn>m(l-n)lnm,
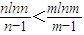
…(8分),
设φ(x)=
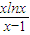
,x>1…(9分),则φ′(x)=
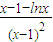
…(10分)
设g(x)=x-l-lnx,则
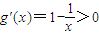
…(11分),g(x)在(1,+∞)上为增函数…(12分),
∴x>1时,g(x)>g(l)=l-l-lnl=0,从而φ′(x)>O,φ(x)在(1,+∞)上为增函数…(13分),
因为m>n>l,所以φ(n)<φ(m),
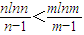
,所以(nm
m)
n>(mn
n)
m…(14分)
点评:本题考查导数知识的运用,考查函数的单调性,考查恒成立问题,考查不等式的证明,正确求导是关键.

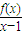 对任意x>l恒成立,求k的最大值;
对任意x>l恒成立,求k的最大值;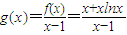 ,求导函数,确定g(x)的最小值,即可求得k的最大值;
,求导函数,确定g(x)的最小值,即可求得k的最大值;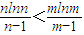 ,构造函数φ(x)=
,构造函数φ(x)=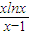 ,x>1,证明φ(x)在(1,+∞)上为增函数即可.
,x>1,证明φ(x)在(1,+∞)上为增函数即可.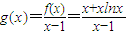 ,则
,则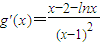 …(6分)
…(6分)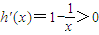 ,∴h(x)在(1,+∞)上是增函数…(8分)
,∴h(x)在(1,+∞)上是增函数…(8分)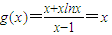 …(13分)
…(13分)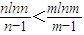 …(8分),
…(8分),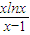 ,x>1…(9分),则φ′(x)=
,x>1…(9分),则φ′(x)=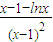 …(10分)
…(10分)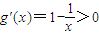 …(11分),g(x)在(1,+∞)上为增函数…(12分),
…(11分),g(x)在(1,+∞)上为增函数…(12分),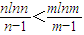 ,所以(nmm)n>(mnn)m…(14分)
,所以(nmm)n>(mnn)m…(14分)

 阅读快车系列答案
阅读快车系列答案