
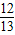 .
.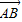 •
•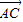 ;
; ,所以先求sinA的值,然后根据三角形面积公式得bc的值.第二问中求a的值,根据第一问中的结论可知,直接利用余弦定理即可.根据同角三角函数关系,由cosA=
,所以先求sinA的值,然后根据三角形面积公式得bc的值.第二问中求a的值,根据第一问中的结论可知,直接利用余弦定理即可.根据同角三角函数关系,由cosA=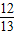 得sinA的值,再根据△ABC面积公式得bc=156;直接求数量积
得sinA的值,再根据△ABC面积公式得bc=156;直接求数量积 •
• .由余弦定理a2=b2+c2-2bccosA,代入已知条件c-b=1,及bc=156求a的值.
.由余弦定理a2=b2+c2-2bccosA,代入已知条件c-b=1,及bc=156求a的值.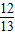 ,得sinA=
,得sinA= =
= .
. sinA=30,∴bc=156.
sinA=30,∴bc=156. •
• =bccosA=156×
=bccosA=156×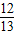 =144.
=144. )=25,
)=25,

科目:高中数学 来源:2010-2011学年广东省湛江市雷州市白沙中学高二(上)段考数学试卷(理科)(解析版) 题型:解答题
 .
. •
• ;
;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com