
分析 (1)化简复数然后求解复数的模.
(2)化简复数,利用复数是纯虚数,实部为0,虚部不为0,求解即可.
解答 解:(1)∵$θ=\frac{4}{3}π$,∴$z=-3cos\frac{4}{3}π+isin\frac{4}{3}π=\frac{3}{2}-\frac{{\sqrt{3}}}{2}i$
∴|z|=$\sqrt{(\frac{3}{2})^{2}+(-\frac{\sqrt{3}}{2})^{2}}$=$\sqrt{3}$.
(2)复数z=-3cosθ+isinθ.复数z1=cosθ-isinθ,
z1z=(-3cosθ+isinθ)(cosθ-isinθ)=-3cos2θ+sin2θ+4icosθsinθ,
z1z为纯虚数,可得:-3cos2θ+sin2θ=0,故tan2θ=3,此时4cosθsinθ≠0,满足题意.
因为$θ∈[\frac{π}{2},π]$,故$tanθ=-\sqrt{3}$,所以$θ=\frac{2π}{3}$.
点评 本题考查复数的基本概念,复数的模的求法,考查计算能力.


 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 16 | B. | 8 | C. | 4 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
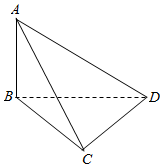 四面体ABCD中,已知AB⊥面BCD,且∠BCD=$\frac{π}{2}$,AB=3,BC=4,CD=5.
四面体ABCD中,已知AB⊥面BCD,且∠BCD=$\frac{π}{2}$,AB=3,BC=4,CD=5.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com