
| cos2x |
| sinx+cosx |
| cos2x |
| sinx+cosx |
| cos2x-sin2x |
| sinx+cosx |
| 2 |
| ||
| 2 |
| ||
| 2 |
| 2 |
| π |
| 4 |
| π |
| 4 |
| π |
| 2 |
| π |
| 4 |
| π |
| 2 |
| 3π |
| 4 |
| π |
| 4 |
| π |
| 2 |
| π |
| 4 |
| 3π |
| 2 |
| π |
| 4 |
| 5π |
| 4 |
| π |
| 4 |
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
| 3π |
| 4 |
| 5π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
| 3π |
| 4 |
| 5π |
| 4 |
| π |
| 4 |


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:高中数学 来源: 题型:
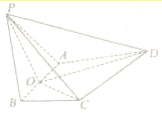 已知四棱锥p-ABCD中,面PAB⊥面ABCD,且BC∥AD,BC⊥AB,且PA=PB=4,AB=2,BC=1,AD=3,O为AB的中点.
已知四棱锥p-ABCD中,面PAB⊥面ABCD,且BC∥AD,BC⊥AB,且PA=PB=4,AB=2,BC=1,AD=3,O为AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
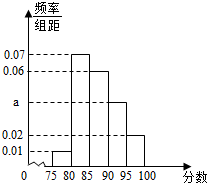 某高校在2014年的自主招生考试成绩中随机抽取100名学生的笔试成绩,
某高校在2014年的自主招生考试成绩中随机抽取100名学生的笔试成绩,查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| 优秀 | 不优秀 | 总计 | |
| 甲班 | 15 | 35 | 50 |
| 乙班 | 10 | 40 | 50 |
| 总计 | 25 | 75 | 100 |
| P(k2>k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com