
【题目】圆x2+y2=4的切线与x轴正半轴,y轴正半轴围成一个三角形,当该三角形面积最小时,切点为P(如图),双曲线C1:![]() 过点P且离心率为
过点P且离心率为 ![]() .
.
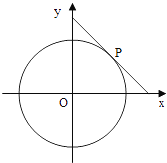
(1)求C1的方程;
(2)若椭圆C2过点P且与C1有相同的焦点,直线l过C2的右焦点且与C2交于A,B两点,若以线段AB为直径的圆过点P,求l的方程.
【答案】(1)![]() (2)
(2)![]()
![]() 或
或 ![]()
【解析】分析:(1)求出出三角形的面积,利用基本不等式的性质可得点![]() 的坐标,将
的坐标,将![]() 的坐标代入双曲线的标准,结合离心率为
的坐标代入双曲线的标准,结合离心率为 ![]() 与
与![]() ,列出关于
,列出关于![]() 、
、![]() 、
、![]() 的方程组,求出
的方程组,求出![]() 、
、![]() 、
、![]() ,即可得结果;(2)由(1)可得椭圆
,即可得结果;(2)由(1)可得椭圆![]() 的焦点,可设椭圆
的焦点,可设椭圆![]() 的方程为
的方程为![]() ,把
,把![]() 的坐标代入即可得出方程,由题意可设直线
的坐标代入即可得出方程,由题意可设直线![]() 的方程为
的方程为![]() 与椭圆方程联立即可得出根与系数的关系,再利用向量垂直与数量积的关系即可得出.
与椭圆方程联立即可得出根与系数的关系,再利用向量垂直与数量积的关系即可得出.
详解:(1)设切点P(x0,y0),(x0>0,y0>0),则切线的斜率为 ![]() ,
,
可得切线的方程为 ![]() ,化为x0x+y0y=4.
,化为x0x+y0y=4.
令x=0,可得 ![]() ;令y=0,可得
;令y=0,可得 ![]() .
.
∴切线与x轴正半轴,y轴正半轴围成一个三角形的面积S= ![]() =
= ![]() .
.
∵4= ![]() ,当且仅当
,当且仅当 ![]() 时取等号.
时取等号.
∴ ![]() .此时P
.此时P ![]() .
.
由题意可得 ![]() ,
, ![]() ,解得a2=1,b2=2.
,解得a2=1,b2=2.
故双曲线C1的方程为 ![]() .
.
(2)由(1)可知双曲线C1的焦点(± ![]() ,0),即为椭圆C2的焦点.
,0),即为椭圆C2的焦点.
可设椭圆C2的方程为 ![]() (b1>0).
(b1>0).
把P ![]() 代入可得
代入可得 ![]() ,解得
,解得 ![]() =3,
=3,
因此椭圆C2的方程为 ![]() .
.
由题意可设直线l的方程为x=my+ ![]() ,A(x1,y1),B(x2,y2),
,A(x1,y1),B(x2,y2),
联立 ![]() ,化为
,化为 ![]() ,
,
∴ ![]() ,
, ![]() .
.
∴x1+x2= ![]() =
= ![]() ,
,
x1x2= ![]() =
= ![]() .
.
![]() ,
, ![]() ,
,
∵ ![]() ,∴
,∴ ![]() ,
,
∴ ![]() +
+ ![]() ,
,
∴ ![]() ,解得m=
,解得m= ![]() -1或m=
-1或m= ![]() ,
,
因此直线l的方程为: ![]() 或
或 ![]()


科目:高中数学 来源: 题型:
【题目】甲、乙、丙三人用擂台赛形式进行训练.每局两人单打比赛,另一人当裁判.每一局的输方去当下一局的裁判,而由原来的裁判向胜者挑战.半天训练结束时,发现甲共打![]() 局,乙共打
局,乙共打![]() 局,而丙共当裁判
局,而丙共当裁判![]() 局.那么整个比赛的第
局.那么整个比赛的第![]() 局的输方( )
局的输方( )
A. 必是甲 B. 必是乙 C. 必是丙 D. 不能确定
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设α,β,γ为两两不重合的平面,l,m,n为两两不重合的直线,给出下列四个命题:
(1)若α⊥γ,β⊥γ,则α//β;
(2)若m![]() α,n
α,n![]() α,
α,![]() , 则α//β;
, 则α//β;
(3)若α//β,l![]() α,则l//β;
α,则l//β;
(4)若![]() , l//γ,则m//n.
, l//γ,则m//n.
其中正确的命题是( )
A.(1)(3)
B.(2)(3)
C.(2)(4)
D.(3)(4)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直四棱柱A1B1C1D1﹣ABCD中,当底面四边形ABCD满足条件 时,有A1C⊥B1D1 . (注:填上你认为正确的一种条件即可,不必考虑所有可能的情形.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点的序列An(xn,0),n∈N*,其中x1=0,x2=a(a>0),A3是线段A1A2的中点,A4是线段A2A3的中点,……,An是线段An-2An-1的中点,……
(1)写出xn与xn-1,xn-2之间的关系式(n≥3);
(2)设an=xn+1-xn,计算a1,a2,a3,由此推测数列{an}的通项公式,并加以证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某机构通过对某企业今年的生产经营情况的调查,得到每月利润![]() (单位:万元)与相应月份数
(单位:万元)与相应月份数![]() 的部分数据如表:
的部分数据如表:
| 1 | 4 | 7 | 12 |
| 229 | 244 | 241 | 196 |
(1)根据如表数据,请从下列三个函数中选取一个恰当的函数描述![]() 与
与![]() 的变化关系,并说明理由,
的变化关系,并说明理由,![]() ,
,![]() ,
,![]() ;
;
(2)利用(1)中选择的函数,估计月利润最大的是第几个月,并求出该月的利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校在2012年的自主招生考试成绩中随机抽取![]() 名中学生的笔试成绩,按成绩分组,得到的频率分布表如表所示.
名中学生的笔试成绩,按成绩分组,得到的频率分布表如表所示.
组号 | 分组 | 频数 | 频率 |
第1组 |
| 5 |
|
第2组 |
| ① |
|
第3组 |
| 30 | ② |
第4组 |
| 20 |
|
第5组 |
| 10 |
|
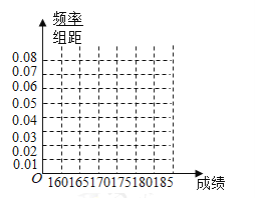
(1)请先求出频率分布表中![]() 位置的相应数据,再完成频率分布直方图;
位置的相应数据,再完成频率分布直方图;
(2)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第![]() 组中用分层抽样抽取名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试;
组中用分层抽样抽取名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试;
(3)在(2)的前提下,学校决定在![]() 名学生中随机抽取
名学生中随机抽取![]() 名学生接受
名学生接受![]() 考官进行面试,求:第
考官进行面试,求:第![]() 组至少有一名学生被考官
组至少有一名学生被考官![]() 面试的概率.
面试的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com