
����Ŀ��ij�����ڽ��д����������еĻ�У�Ϊ�˽����ԡ����ġ�������̶ȣ���֯��������֣�����Ϊ����������Ϊ100�֣������������ȡһ������Ϊ120�������������������ݾ���![]() �ڣ��ֽ���Щ�����ֳ�����6�鲢������������Ƶ�ʷֲ�ֱ��ͼ������С�������˲���ͼ�Σ���ͼ��ʾ���۲�ͼ�Σ��ش��������⣺
�ڣ��ֽ���Щ�����ֳ�����6�鲢������������Ƶ�ʷֲ�ֱ��ͼ������С�������˲���ͼ�Σ���ͼ��ʾ���۲�ͼ�Σ��ش��������⣺
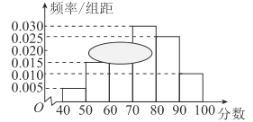
��1�����������![]() ��Ƶ��������ȫƵ�ʷֲ�ֱ��ͼ��
��Ƶ��������ȫƵ�ʷֲ�ֱ��ͼ��
��2�������Ƶ�ʷֲ�ֱ��ͼ��������������������λ����ƽ��������ÿ��������������е�ֵΪ������
���𰸡���1��18�ˣ�����������2������Ϊ75�֣���λ��Ϊ75�֣�ƽ����Ϊ73.5��
��������
��1�������������![]() �ڵ�Ƶ�ʣ����������
�ڵ�Ƶ�ʣ����������![]() ��Ƶ��,��ȫƵ�ʷֲ�ֱ��ͼ��(2)����Ƶ�ʷֲ�ֱ��ͼ�е���������λ����ƽ��������ⷽ����⼴��.
��Ƶ��,��ȫƵ�ʷֲ�ֱ��ͼ��(2)����Ƶ�ʷֲ�ֱ��ͼ�е���������λ����ƽ��������ⷽ����⼴��.
��1����Ϊ�����Ƶ��֮�͵���1�����Է�����![]() �ڵ�Ƶ��Ϊ��
�ڵ�Ƶ��Ϊ��
![]() ��
��
���Ե�����![]() �Ķ���Ϊ
�Ķ���Ϊ![]() ���ˣ���������Ƶ�ʷֲ�ֱ��ͼ��ͼ��
���ˣ���������Ƶ�ʷֲ�ֱ��ͼ��ͼ��
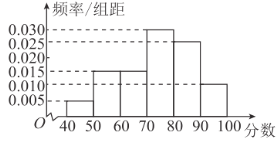
��2����Ϊ�����Ĺ���ֵ��Ƶ�ʷֲ�ֱ��ͼ����߾��ε��е㣬��ͼ�пɿ��������Ĺ���ֵΪ75�֣�
�������ߵ�һ�����ε����Ϊ0.05���ڶ������ε����Ϊ0.15,���������ε����Ϊ0.15,���ĸ����ε����Ϊ0.3��������λ���ڵ��ĸ��������棬����λ��Ϊx,
��0.05+0.15+0.15+(x-70)��0.03=0.5��
����x=75.������λ��Ϊ75.
�ָ���Ƶ�ʷֲ�ֱ��ͼ��������ƽ�����Ĺ���ֵΪ��![]() ���֣���
���֣���
��������������Ϊ75�֣���λ��Ϊ75�֣�ƽ����Ϊ73.5�֣�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ѧ��ŷ����1765�귢�֣����������ε����ġ����ġ�����λ��ͬһ��ֱ���ϣ�����ֱ�߳�Ϊŷ������֪![]() �Ķ���
�Ķ���![]() ������ŷ���ߵķ���Ϊ
������ŷ���ߵķ���Ϊ![]() ����
����![]() �������� ��
�������� ��
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2018��Ϊ�ҹ��ĸ↑��40���꣬ij��ҵ��λ����ְ��600�ˣ��������������ֲ������£�
����� |
|
|
|
|
��������λ���ˣ� | 180 | 180 | 160 | 80 |
Լ�����˵�λ45��~59��Ϊ�����ˣ�����Ϊ�����ˣ��ְ��շֲ������ȡ30����Ϊȫ����ף����Ĺ���.
��1����������������������ڷֱ�Ϊ�����ˣ�
��2��������ȡ���������������������зֱ���12�˺�5�˲����Թ����������£����������Թ�����������.�������![]() �����������ش��ܷ���
�����������ش��ܷ���![]() �İ�����Ϊ����������Թ������������йأ�
�İ�����Ϊ����������Թ������������йأ�
���Թ����������� | �����Թ����������� | �ܼ� | |
���� | 12 | ||
���� | 5 | ||
�ܼ� | 30 |
��3���������Թ����������µ�������ڣ�����1���ó����裬3���ó��������У������ȡ2����̨���ݽ�Ŀ��������2����ʤ�β��ձ��ݵĸ����Ƕ��٣�
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
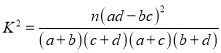 .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ABC����a=7��b=8��cosB= �C![]() ��
��
����������A��
��������AC���ϵĸ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�����Σ�AD��BC����BAD=90�㣬�ı���CC1D1DΪ���Σ���֪AB��BC1��AD=4��AB=2��BC=1.
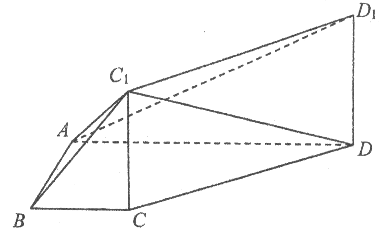
��I����֤��BC1��ƽ��ADD1��
��II����DD1=2����ƽ��AC1D1��ƽ��ADD1���ɵ������ǵ�����ֵ��
��III����PΪ�߶�C1D�ϵ�һ�����㣨�˵���⣩���ж�ֱ��BC1��ֱ��CP�ܷ�ֱ?��˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ԲC�� ![]() ��a>b>0����������Ϊ
��a>b>0����������Ϊ![]() ��FΪ��ԲC���ҽ���.A��-a��0����|AF|=3.
��FΪ��ԲC���ҽ���.A��-a��0����|AF|=3.
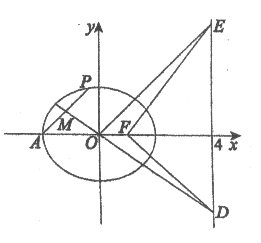
��I������ԲC�ķ��̣�
��II����OΪԭ�㣬PΪ��Բ��һ�㣬AP���е�ΪM.ֱ��OM��ֱ��x=4���ڵ�D����O��ƽ����AP��ֱ����ֱ��x=4���ڵ�E.��֤����ODF=��OEF.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��1642�꣬��˹��������һ�ֿ��Խ���ʮ���ƼӼ����Ļ�е�����![]() �꣬������ĸĽ�����˹���ļ������������������Ϊʮ���Ƶ������ڼ������ʵ���������ڸ��ӣ��漴����ˡ������ơ����ĸ���
�꣬������ĸĽ�����˹���ļ������������������Ϊʮ���Ƶ������ڼ������ʵ���������ڸ��ӣ��漴����ˡ������ơ����ĸ���![]() ֮�����ǶԽ�λ�Ƶ�Ч�����������������о�
֮�����ǶԽ�λ�Ƶ�Ч�����������������о�![]() �о��������£�����������
�о��������£�����������![]() ��
��![]() ��������
��������![]() �Ų�ͬ�Ŀ�Ƭ������д������0��1������
�Ų�ͬ�Ŀ�Ƭ������д������0��1������![]() �Ŀ�Ƭ����
�Ŀ�Ƭ����![]() ��
��![]() �������Щ��Ƭ��ʾ
�������Щ��Ƭ��ʾ![]() λ
λ![]() ��������ͨ����ͬ�Ŀ�Ƭ��ϣ���Щ��Ƭ���Ա�ʾ
��������ͨ����ͬ�Ŀ�Ƭ��ϣ���Щ��Ƭ���Ա�ʾ![]() ����ͬ������
����ͬ������![]() ����
����![]() ��
��![]() ʱ�����ǿ��Ա�ʾ��
ʱ�����ǿ��Ա�ʾ��![]() ��
��![]() ����ͬ������
����ͬ������![]() ���迨Ƭ������
���迨Ƭ������![]() Ϊһ����ֵ����ô
Ϊһ����ֵ����ô![]() ���Ƶ�Ч���������ζ��
���Ƶ�Ч���������ζ��![]() �ſ�Ƭ����ʾ�IJ�ͬ�����ĸ���
�ſ�Ƭ����ʾ�IJ�ͬ�����ĸ���![]() ���
���![]() ���������о������������Ƶ�Ч����ߣ�
���������о������������Ƶ�Ч����ߣ�![]() ����
����![]()
A. ������ B. ������ C. ʮ���� D. ʮ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ϵ������Ϊ![]() ����ָ�����ʳ��֧��ռ��ͥ������֧���ı���.�����ϳ��ö����ϵ��������һ�����Һ͵�����������ˮƽ��״��.���Ϲ�������ˮƽ�Ĺ涨�����±���
����ָ�����ʳ��֧��ռ��ͥ������֧���ı���.�����ϳ��ö����ϵ��������һ�����Һ͵�����������ˮƽ��״��.���Ϲ�������ˮƽ�Ĺ涨�����±���
��ͥ���� | ƶ�� | �±� | С�� | ��ԣ | �ԣ |
|
|
|
|
|
|
ʵʩ����ƶ���������ݶ�ijɽ��ƶ����ͥ����֧���������λ����Ԫ���ij������飬2018��ÿ����ͥƽ������֧���ܶ�Ϊ2��Ԫ������ʳ������֧��Ϊ1.2��ԪԤ��2018�굽2020��ÿ����ͥƽ������֧���ܶ�ÿ���������Լ��30%����ʳ������֧��ƽ��ÿ������0.2��Ԫ��Ԥ���ɽ���ļ�ͥ2020�꽫���ڣ� ��
A.ƶ��ˮƽB.�±�ˮƽC.С��ˮƽD.��ԣˮƽ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x����lnx![]() x2��g��x��
x2��g��x��![]() x2+x��m��R����F��x����f��x��+g��x����
x2+x��m��R����F��x����f��x��+g��x����
��������f��x���ĵ����������䣻
����������x�IJ���ʽF��x����mx��1�������������m����Сֵ��
������m����1������ʵ��x1��x2����F��x1������F��x2������֤��x1+x2![]() 1��
1��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com