练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知f(x)是定义在(0,+∞)上的增函数,f(x)＞0且f(3)=1,指出函数F(x)=f(x)+(x＞0)的单调区间,并加以证明.?

    思路分析:这道题要求先写出单调区间,但单调区间无法从函数解析式上观察出来.也无法画出函数的图象,再从图象上看出来.故只能根据函数的单调性的定义,直接进行演绎推理.由已知条件f(3)=1,猜测:3可能是单调区间的一个端点.?

    解:设0＜x1＜x2,则?

    F(x2)-F(x1)=f(x2)+-［f(x1)+］

    =［f(x2)-f(x1)］·［1-］.?

    当0＜x1＜x2≤3时,0＜f(x1)＜f(x2)≤f(3) =1,?

    ∴f(x2)-f(x1)＞0,1-＜0.?

    ∴F(x2)-F(x1)＜0,F(x2)＜F(x1).?

    ∴F(x)在(0,3］上是减函数.?

    当3≤x1＜x2时,1=f(3)≤f(x1)＜f(x2),?

    ∴f(x2)-f(x1)＞0,1-＞0.?

    ∴F(x2)-F(x1)＞0,F(x2)＞F(x1).?

    ∴F(x)在［3,+∞)上是增函数.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    下列结论中正确的是
    ①②③
    ①②③
    ．
    ①函数y=f（x）是定义在R上的偶函数，且f（x+1）=-f（x），则函数y=f（x）的图象关于直线x=1对称；
    ②已知ξ～N（16，σ2），若P（ξ＞17）=0.35，则P（15＜ξ＜16）=0.15；
    ③
    已知f(x)是定义在(-∞，+∞)上的偶函数，且在(-∞，0]上是增函数．设a=f(ln
    1
    3
    )，b=f(log43)，
    c=f(0.4-1.2)，则c＜a＜b；

    ④线性相关系数r的绝对值越接近于1，表明两个变量线性相关程度越弱．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知f(x)是定义在实数集R上的函数,它的反函数为f-1(x),若y=f-1(x+1)与y=f(x+1)互为反函数,且f(1)=1,则f(2)的值为

    A.2                  B.1                   C.0                   D.-1

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知f(x)是定义在R上的不恒为零的函数，且对于任意的a,b∈R,满足f(a·b)=af(b)+bf(a),f(2)=2,a=(n∈N*),b=(n∈N*);考查下列结论：

    ①f(0)=f(1);②f(x)为偶函数；③数列{a}为等比数列；④{b}为等差数列.

    其中正确的是               .

    查看答案和解析>>

    科目：高中数学 来源：2015届广东省高一第一次阶段考试数学试卷（解析版） 题型：解答题

    （本小题满分14分）已知f(x)是定义在( 0，＋∞)上的增函数，

    且f() = f(x)－f(y)  

    （1）求f(1)的值;

    （2）若f(6)= 1，解不等式 f( x＋3 )－f(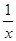) ＜2

     

    查看答案和解析>>

    科目：高中数学 来源：2010年黑龙江省高一上学期期末考试数学试卷 题型：填空题

    已知f (x)是定义在∪上的奇函数，当时，f (x)的图象如图所示，那么f (x)的值域是                   

     

    查看答案和解析>>

    同步练习册答案