
【题目】抛物线![]() 的焦点为
的焦点为![]() ,
,![]() 是抛物线上关于
是抛物线上关于![]() 轴对称的两点,点
轴对称的两点,点![]() 是抛物线准线
是抛物线准线![]() 与
与![]() 轴的交点,
轴的交点,![]() 是面积为
是面积为![]() 的直角三角形.
的直角三角形.
(1)求抛物线的方程;
(2)点![]() 在抛物线上,
在抛物线上,![]() 是直线
是直线![]() 上不同的两点,且线段
上不同的两点,且线段![]() 的中点都在抛物线上,试用
的中点都在抛物线上,试用![]() 表示
表示![]() .
.
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:高中数学 来源: 题型:
【题目】(1)已知数列![]() 的通项公式:
的通项公式:![]() ,试求
,试求![]() 最大项的值;
最大项的值;
(2)记![]() ,且满足(1),若
,且满足(1),若![]() 成等比数列,求p的值;
成等比数列,求p的值;
(3)如果![]() ,
,![]() ,
,![]() ,且p是满足(2)的正常数,试证:对于任意自然数n,或者都满足
,且p是满足(2)的正常数,试证:对于任意自然数n,或者都满足![]() ,
,![]() ,或者都满足
,或者都满足![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某小区有一块三角形空地,如图△ABC,其中AC=180米,BC=90米,∠C=90°,开发商计划在这片空地上进行绿化和修建运动场所,在△ABC内的P点处有一服务站(其大小可忽略不计),开发商打算在AC边上选一点D,然后过点P和点D画一分界线与边AB相交于点E,在△ADE区域内绿化,在四边形BCDE区域内修建运动场所. 现已知点P处的服务站与AC距离为10米,与BC距离为100米. 设![]() 米,试问
米,试问![]() 取何值时,运动场所面积最大?
取何值时,运动场所面积最大?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线C的参数方程为![]() (α为参数),在以坐标原点O为极点,x轴的正半轴为极轴的极坐标系中,点P的极坐标为
(α为参数),在以坐标原点O为极点,x轴的正半轴为极轴的极坐标系中,点P的极坐标为![]() ,直线l的极坐标方程为
,直线l的极坐标方程为![]() .
.
(1)求直线l的直角坐标方程与曲线C的普通方程;
(2)若Q是曲线C上的动点,M为线段PQ的中点,直线l上有两点A,B,始终满足|AB|=4,求△MAB面积的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设抛物线![]() 的焦点为
的焦点为![]() ,经过
,经过![]() 轴正半轴上点
轴正半轴上点![]() 的直线
的直线![]() 交
交![]() 于不同的两点
于不同的两点![]() 和
和![]() .
.
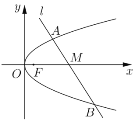
(1)若![]() ,求点
,求点![]() 的坐标;
的坐标;
(2)若![]() ,求证:原点
,求证:原点![]() 总在以线段
总在以线段![]() 为直径的圆的内部;
为直径的圆的内部;
(3)若![]() ,且直线
,且直线![]() ∥
∥![]() ,
,![]() 与
与![]() 有且只有一个公共点
有且只有一个公共点![]() ,问:△
,问:△![]() 的面积是否存在最小值?若存在,求出最小值,并求出
的面积是否存在最小值?若存在,求出最小值,并求出![]() 点的坐标,若不存在,请说明理由.
点的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的三个内角A,B,C所对的边分别是a,b,c,向量![]() =(cos B,cos C),
=(cos B,cos C),![]() =(2a+c,b),且
=(2a+c,b),且![]() ⊥
⊥![]() .
.
(1)求角B的大小;
(2)若b=![]() ,求a+c的范围.
,求a+c的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场举行购物抽奖促销活动,规定每位顾客从装有0、1、2、3的四个相同小球的抽奖箱中,每次取出一球记下编号后放回(连续取两次),若取出的两个小球的编号相加之和等于6,则中一等奖,等于5中二等奖,等于4或3中三等奖,则顾客抽奖中三等奖的概率为____________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com