
【题目】一只红玲虫的产卵数![]() 和温度
和温度![]() 有关.现收集了7组观测数据如下表:
有关.现收集了7组观测数据如下表:
温度 | 21 | 23 | 25 | 27 | 29 | 32 | 35 |
产卵数 | 7 | 11 | 21 | 24 | 66 | 115 | 325 |
为了预报一只红玲虫在![]() 时的产卵数,根据表中的数据建立了
时的产卵数,根据表中的数据建立了![]() 与
与![]() 的两个回归模型.模型①:先建立
的两个回归模型.模型①:先建立![]() 与
与![]() 的指数回归方程
的指数回归方程![]() ,然后通过对数变换
,然后通过对数变换![]() ,把指数关系变为
,把指数关系变为![]() 与
与![]() ;模型②:先建立
;模型②:先建立![]() 与
与![]() 的二次回归方程
的二次回归方程![]() ,然后通过变换
,然后通过变换![]() ,把二次关系变为
,把二次关系变为![]() 与
与![]() 的线性回归方程:
的线性回归方程:![]() .
.
(1)分别利用这两个模型,求一只红玲虫在![]() 时产卵数的预测值;
时产卵数的预测值;
(2)你认为用哪个模型得到的预测值更可靠?并说明理由.(参考数据:模型①的残差平方和![]() ,模型①的相关指数
,模型①的相关指数![]() ;模型②的残差平方和
;模型②的残差平方和![]() ,模型②的相关指数
,模型②的相关指数![]() ;
;![]() ,
,![]() ,
,![]() ;
;![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
【答案】(1)![]() ,
,![]() (2)模型①得到的预测值更可靠,理由见解析
(2)模型①得到的预测值更可靠,理由见解析
【解析】
(1)把![]() 分别代入两个模型求解即可;
分别代入两个模型求解即可;
(2)通过残差及相关指数的大小进行判定比较.
(1)当![]() 时,根据模型①,得
时,根据模型①,得![]() ,
, ![]() ,根据模型②,得
,根据模型②,得![]() .
.
(2)模型①得到的预测值更可靠.理由1:因为模型①的残差平方和![]() 小于模型②的残差平方和
小于模型②的残差平方和![]() ,所以模型①得到的预测值比模型②得到的预测值更可靠;理由2:模型①的相关指数
,所以模型①得到的预测值比模型②得到的预测值更可靠;理由2:模型①的相关指数![]() 大于模型②的相关指数
大于模型②的相关指数![]() ,所以模型①得到的预测值比模型②得到的预测值更可靠;理由3:因为由模型①,根据变换后的线性回归方程
,所以模型①得到的预测值比模型②得到的预测值更可靠;理由3:因为由模型①,根据变换后的线性回归方程![]() 计算得到的样本点分布在一条直线的附近;而由模型②,根据变换后的线性回归方程
计算得到的样本点分布在一条直线的附近;而由模型②,根据变换后的线性回归方程![]() 得到的样本点不分布在一条直线的周围,因此模型②不适宜用来拟合
得到的样本点不分布在一条直线的周围,因此模型②不适宜用来拟合![]() 与
与![]() 的关系;所以模型①得到的预测值比模型②得到的预测值更可靠.(注:以上给出了3种理由,考生答出其中任意一种或其他合理理由均可得)
的关系;所以模型①得到的预测值比模型②得到的预测值更可靠.(注:以上给出了3种理由,考生答出其中任意一种或其他合理理由均可得)


科目:高中数学 来源: 题型:
【题目】已如椭圆C:![]() 的两个焦点与其中一个顶点构成一个斜边长为4的等腰直角三角形.
的两个焦点与其中一个顶点构成一个斜边长为4的等腰直角三角形.
(1)求椭圆C的标准方程;
(2)设动直线l交椭圆C于P,Q两点,直线OP,OQ的斜率分别为k,k'.若![]() ,求证△OPQ的面积为定值,并求此定值.
,求证△OPQ的面积为定值,并求此定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() ,若圆
,若圆![]()
![]() 的一条切线与椭圆
的一条切线与椭圆![]() 有两个交点
有两个交点![]() ,且
,且![]() .
.

(1)求圆![]() 的方程;
的方程;
(2)已知椭圆![]() 的上顶点为
的上顶点为![]() ,点
,点![]() 在圆
在圆![]() 上,直线
上,直线![]() 与椭圆
与椭圆![]() 相交于另一点
相交于另一点![]() ,且
,且![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某花圃为提高某品种花苗质量,开展技术创新活动,在![]() 实验地分别用甲、乙方法培育该品种花苗.为观测其生长情况,分别在实验地随机抽取各50株,对每株进行综合评分,将每株所得的综合评分制成如图所示的频率分布直方图,记综合评分为80及以上的花苗为优质花苗.
实验地分别用甲、乙方法培育该品种花苗.为观测其生长情况,分别在实验地随机抽取各50株,对每株进行综合评分,将每株所得的综合评分制成如图所示的频率分布直方图,记综合评分为80及以上的花苗为优质花苗.

(1)求图中![]() 的值,并估计该品种花苗综合评分的平均数(同一组中的数据用该组区间的中点值为代表);
的值,并估计该品种花苗综合评分的平均数(同一组中的数据用该组区间的中点值为代表);
(2)填写下面的列联表,并判断是否有99%的把握认为优质花苗与培驻外方法有关.
优质花苗 | 非优质花苗 | 合计 | |
甲培育法 | 20 | ||
乙培育法 | 10 | ||
合计 |
附:下面的临界值表仅供参考.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
(参考公式: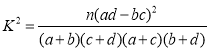 ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现计划用两张铁丝网在一片空地上围成一个梯形养鸡场![]() ,
,![]() ,
,![]() ,已知
,已知![]()
![]() 两段是由长为
两段是由长为![]() 的铁丝网折成,
的铁丝网折成,![]()
![]() 两段是由长为
两段是由长为![]() 的铁丝网折成.设上底
的铁丝网折成.设上底![]() 的长为
的长为![]() ,所围成的梯形面积为
,所围成的梯形面积为![]() .
.
(1)求S关于x的函数解析式,并求x的取值范围;
(2)当x为何值时,养鸡场的面积最大?最大面积为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》中《方田》章有弧田面积计算问题,计算术曰:以弦乘矢,矢又自乘,并之,二而一.其大意是,弧田面积计算公式为:弧田面积![]() (弦乘矢+矢乘矢),弧田是由圆弧(简称为弧田的弧)和以圆弧的端点为端点的线段(简称 (弧田的弦)围成的平面图形,公式中“弦”指的是弧田的弦长,“矢”等于弧田的弧所在圆的半径与圆心到弧田的弦的距离之差.现有一弧田,其弦长
(弦乘矢+矢乘矢),弧田是由圆弧(简称为弧田的弧)和以圆弧的端点为端点的线段(简称 (弧田的弦)围成的平面图形,公式中“弦”指的是弧田的弦长,“矢”等于弧田的弧所在圆的半径与圆心到弧田的弦的距离之差.现有一弧田,其弦长![]() 等于
等于![]() ,其弧所在圆为圆
,其弧所在圆为圆![]() ,若用上述弧田面积计算公式计算得该弧田的面积为
,若用上述弧田面积计算公式计算得该弧田的面积为![]() ,则
,则![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,则下列关于函数
,则下列关于函数![]() 的说法,不正确的是( )
的说法,不正确的是( )
A.![]() 的图象关于
的图象关于![]() 对称
对称
B.![]() 在
在![]() 上有2个零点
上有2个零点
C.![]() 在区间
在区间![]() 上单调递减
上单调递减
D.函数![]() 图象向右平移
图象向右平移![]() 个单位,所得图像对应的函数为奇函数
个单位,所得图像对应的函数为奇函数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com