
本小题满分12分)设M是由满足下列条件的函数f (x)构成的集合:①方程f (x)一x=0有实根;②函数的导数 满足0<
满足0< <1.
<1.
(1)若函数f(x)为集合M中的任意一个元素,证明:方程f(x)一x=0只有一个实根;
(2)判断函数 是否是集合M中的元素,并说明理由;
是否是集合M中的元素,并说明理由;
(3)设函数f(x)为集合M中的任意一个元素,对于定义域中任意 ,
,
证明:
(1)令 ,则
,则 ,故
,故 是单调递减函数,
是单调递减函数,
所以,方程 ,即
,即 至多有一解,又由题设①知方程
至多有一解,又由题设①知方程 有实数根,所以,方程
有实数根,所以,方程 有且只有一个实数根;(2)
有且只有一个实数根;(2) ;(Ⅲ)不妨设
;(Ⅲ)不妨设 ,∵
,∵ ,∴
,∴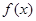 单调递增,∴
单调递增,∴ ,即
,即 ,
,
令 ,则
,则 ,故
,故 是单调递减函数,
是单调递减函数,
∴ ,即
,即 ,
,
∴ ,则有
,则有
解析试题分析:令 ,则
,则 ,故
,故 是单调递减函数,
是单调递减函数,
所以,方程 ,即
,即 至多有一解,
至多有一解,
又由题设①知方程 有实数根,
有实数根,
所以,方程 有且只有一个实数根…………………………………..4分
有且只有一个实数根…………………………………..4分
(2)易知, ,满足条件②;
,满足条件②;
令 ,
,
则 ,…………………………………..7分
,…………………………………..7分
又 在区间
在区间 上连续,所以
上连续,所以 在
在 上存在零点
上存在零点 ,
,
即方程 有实数根
有实数根 ,故
,故 满足条件①,
满足条件①,
综上可知, ……………………………………8分
……………………………………8分
(Ⅲ)不妨设 ,∵
,∵ ,∴
,∴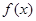 单调递增,
单调递增,
∴ ,即
,即 ,
,
令 ,则
,则 ,故
,故 是单调递减函数,
是单调递减函数,
∴ ,即
,即 ,
,
∴ ,则有
,则有 ….……………..….12分
….……………..….12分
考点:本题考查了导数的运用
点评:近几年新课标高考对于函数与导数这一综合问题的命制,一般以有理函数与半超越(指数、对数)函数的组合复合且含有参量的函数为背景载体,解题时要注意对数式对函数定义域的隐蔽,这类问题重点考查函数单调性、导数运算、不等式方程的求解等基本知识,注重数学思想(分类与整合、数与形的结合)方法(分析法、综合法、反证法)的运用.把数学运算的“力量”与数学思维的“技巧”完美结合.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案科目:高中数学 来源: 题型:解答题
已知f(x)=x- (a>0),g(x)=2lnx+bx且直线y=2x-2与曲线y=g(x)相切.
(a>0),g(x)=2lnx+bx且直线y=2x-2与曲线y=g(x)相切.
(1)若对[1,+ )内的一切实数x,小等式f(x)≥g(x)恒成立,求实数a的取值范围;
)内的一切实数x,小等式f(x)≥g(x)恒成立,求实数a的取值范围;
(2)当a=l时,求最大的正整数k,使得对[e,3](e=2.71828是自然对数的底数)内的任意k个实数x1,x2,,xk都有 成立;
成立;
(3)求证: .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题14分) 已知函数f(x)=ax3+bx2+cx(a≠0)是定义在R上的奇函数,且x=-1时,函数取极值1。
(1)求a,b,c的值;
(2)若x1,x2∈[-1,1],求证:|f(x1)-f(x2)|≤2;
(3)求证:曲线y=f(x)上不存在两个不同的点A,B,使过A, B两点的切线都垂直于直线AB。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分12分)已知函数
(1)当 时,求函数
时,求函数 的单调区间;
的单调区间;
(2)若函数 的图像在点
的图像在点 处的切线的倾斜角为
处的切线的倾斜角为 ,问:
,问: 在什么范围取值时,对于任意的
在什么范围取值时,对于任意的 ,函数
,函数 在区间
在区间 上总存在极值?
上总存在极值?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com