
如图,两个不全等的△ABC与△A1B1C1分别在两个互相平行的平面内,它们的边两两对应平行,求证:多面体A1B1C1-ABC为棱台.
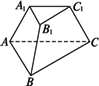
|
证明:∵A1B1∥AB,∴A1B1与AB确定平面α. 同理,B1C1与BC确定平面β,C1A1与CA确定平面γ.又∵△ABC与△A1B1C1不全等,∴A1B1≠AB. ∴平面α内的两直线AA1与BB1必相交,不妨设交点为P.∴P∈AA1 ∴P∈β∩γ=CC1.∴AA1、BB1与CC1延长后相交于一点(如下图所示).
∴P-ABC为三棱锥. ∵△A1B1C1是被平行于ABC所在的平面所截, ∴多面体A1B1C1-ABC为棱台. |
|
按棱台的定义,要证明一个多面体是一个棱台,首先应证明这里包含有一个棱锥,故必须首先证明AA1、BB1、CC1相交于一点,其次说明两平面平行(这一点是已知的),进而可解决问题. |


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:
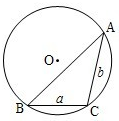 通常用a、b、c表示△ABC的三个内角∠A、∠B、∠C所对边的边长,R表示△ABC外接圆半径.
通常用a、b、c表示△ABC的三个内角∠A、∠B、∠C所对边的边长,R表示△ABC外接圆半径.查看答案和解析>>
科目:高中数学 来源:设计必修二数学苏教版 苏教版 题型:047
如图所示,两个不全等的△ABC与△A1B1C1分别在两个互相平行的平面内,它们的边两两对应平行.求证:多面体A1B1C1-ABC为棱台.

查看答案和解析>>
科目:高中数学 来源:2009-2010学年湖北省武汉二中高一(上)期末数学试卷(解析版) 题型:解答题

查看答案和解析>>
科目:高中数学 来源:2007年上海市春季高考数学试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com