
【题目】已知椭圆![]()
![]() 经过点
经过点![]() ,一个焦点是
,一个焦点是![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若倾斜角为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,且
两点,且![]() ,求直线
,求直线![]() 的方程.
的方程.
科目:高中数学 来源: 题型:
【题目】某小学为了解本校某年级女生的身高情况,从本校该年级的学生中随机选出100名女生并统计她们的身高(单位: ![]() ),得到如图频率分布表:
),得到如图频率分布表:
分组(身高) |
|
|
|
|
(Ⅰ)用分层抽样的方法从身高在![]() 和
和![]() 的女生中共抽取6人,则身高在
的女生中共抽取6人,则身高在![]() 的女生应抽取几人?
的女生应抽取几人?
(Ⅱ)在(Ⅰ)中抽取的6人中,再随机抽取2人,求这2人身高都在![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|< ![]() )的部分图象如图所示,若将f(x)的图象上所有点向右平移
)的部分图象如图所示,若将f(x)的图象上所有点向右平移 ![]() 个单位得到函数g(x)的图象,则函数g(x)的单调增区间为( )
个单位得到函数g(x)的图象,则函数g(x)的单调增区间为( ) 
A.![]() ,k∈Z
,k∈Z
B.![]() ,k∈Z
,k∈Z
C.![]() ,k∈Z
,k∈Z
D.![]() ,k∈Z
,k∈Z
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系中,已知点![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为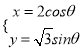 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,点
轴正半轴为极轴,建立极坐标系,点![]() 的极坐标为
的极坐标为![]() ,直线
,直线![]() 的极坐标方程为
的极坐标方程为![]() ,且
,且![]() 过点
过点![]() ;过点
;过点![]() 与直线
与直线![]() 平行的直线为
平行的直线为![]() ,
, ![]() 与曲线
与曲线![]() 相交于两点
相交于两点![]() .
.
(1)求曲线![]() 上的点到直线
上的点到直线![]() 距离的最小值;
距离的最小值;
(2)求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,隔河看两目标A、B,但不能到达,在岸边选取相距 ![]() km的C、D两点,并测得∠ACB=75°,∠BCD=45°,∠ADC=30°,∠ADB=45°(A、B、C、D在同一平面内),求两目标A、B之间的距离.
km的C、D两点,并测得∠ACB=75°,∠BCD=45°,∠ADC=30°,∠ADB=45°(A、B、C、D在同一平面内),求两目标A、B之间的距离. 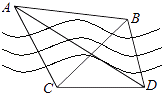
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面向量 ![]() =(1,x),
=(1,x), ![]() =(2x+3,﹣x)(x∈R).
=(2x+3,﹣x)(x∈R).
(1)若 ![]() ∥
∥ ![]() ,求|
,求| ![]() |
|
(2)若 ![]() 与
与 ![]() 夹角为锐角,求x的取值范围.
夹角为锐角,求x的取值范围.
(3)若| ![]() |=2,求与
|=2,求与 ![]() 垂直的单位向量
垂直的单位向量 ![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com