
【题目】一个口袋中装有![]() 个红球
个红球![]() 且
且![]() 和
和![]() 个白球,一次摸奖从中摸两个球,两个球颜色不同则为中奖.
个白球,一次摸奖从中摸两个球,两个球颜色不同则为中奖.
(1)用![]() 表示一次摸奖中奖的概率
表示一次摸奖中奖的概率![]() ;
;
(2)若![]() ,设三次摸奖(每次摸奖后球放回)恰好有
,设三次摸奖(每次摸奖后球放回)恰好有![]() 次中奖,求
次中奖,求![]() 的数学期望
的数学期望![]() ;
;
(3)设三次摸奖(每次摸奖后球放回)恰好有一次中奖的概率![]() ,当
,当![]() 取何值时,
取何值时, ![]() 最大?
最大?
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】已知在平面直角坐标系![]() 中,
中, ![]() 为坐标原点,曲线
为坐标原点,曲线![]() :
: 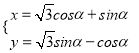 (
(![]() 为参数),在以平面直角坐标系的原点为极点,
为参数),在以平面直角坐标系的原点为极点, ![]() 轴的正半轴为极轴,取相同单位长度的极坐标系,直线
轴的正半轴为极轴,取相同单位长度的极坐标系,直线![]() :
: ![]() .
.
(Ⅰ)求曲线![]() 的普通方程和直线
的普通方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)曲线![]() 上恰好存在三个不同的点到直线
上恰好存在三个不同的点到直线![]() 的距离相等,分别求出这三个点的极坐标.
的距离相等,分别求出这三个点的极坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两名选手参加歌手大赛时,5名评委打的分数用茎叶图表示(如图).s1、s2分别表示甲、乙选手分数的标准差,则s1与s2的关系是( ) 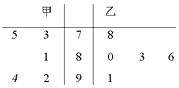
A.s1>s2
B.s1=s2
C.s1<s2
D.不确定
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】排列组合
(1)7位同学站成一排,甲、乙两同学必须相邻的排法共有多少种?
(2)7位同学站成一排,甲、乙和丙三个同学都不能相邻的排法共有多少种?
(3)7位同学站成一排,甲不站排头,乙不站排尾,不同站法种数有多少种?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了得到函数 ![]() 的图象,只要将函数y=sin2x的图象( )
的图象,只要将函数y=sin2x的图象( )
A.向右平移 ![]() 个单位长度
个单位长度
B.向左平移 ![]() 个单位长度
个单位长度
C.向右平移 ![]() 个单位长度
个单位长度
D.向左平移 ![]() 个单位长度
个单位长度
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我们称满足: ![]() (
(![]() )的数列
)的数列![]() 为“
为“![]() 级梦数列”.
级梦数列”.
(1)若![]() 是“
是“![]() 级梦数列”且
级梦数列”且![]() .求:
.求: ![]() 和
和![]() 的值;
的值;
(2)若![]() 是“
是“![]() 级梦数列”且满足
级梦数列”且满足![]() ,
, ![]() ,求
,求![]() 的最小值;
的最小值;
(3)若![]() 是“0级梦数列”且
是“0级梦数列”且![]() ,设数列
,设数列![]() 的前
的前![]() 项和为
项和为![]() .证明:
.证明: ![]() (
(![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的离心率为
的离心率为![]() ,以椭圆长、短轴四个端点为顶点为四边形的面积为
,以椭圆长、短轴四个端点为顶点为四边形的面积为![]() .
.
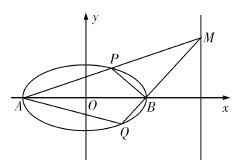
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)如图所示,记椭圆的左、右顶点分别为![]() 、
、![]() ,当动点
,当动点![]() 在定直线
在定直线![]() 上运动时,直线
上运动时,直线![]() 分别交椭圆于两点
分别交椭圆于两点![]() 、
、![]() ,求四边形
,求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com