
【题目】定义:f1(x)=f(x),当n≥2且x∈N*时,fn(x)=f(fn﹣1(x)),对于函数f(x)定义域内的x0 , 若正在正整数n是使得fn(x0)=x0成立的最小正整数,则称n是点x0的最小正周期,x0称为f(x)的n~周期点,已知定义在[0,1]上的函数f(x)的图象如图,对于函数f(x),下列说法正确的是(写出所有正确命题的编号)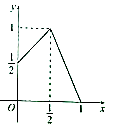
①1是f(x)的一个3~周期点;
②3是点 ![]() 的最小正周期;
的最小正周期;
③对于任意正整数n,都有fn( ![]() )=
)= ![]() ;
;
④若x0∈( ![]() ,1],则x0是f(x)的一个2~周期点.
,1],则x0是f(x)的一个2~周期点.
【答案】①②③
【解析】解:f1(1)=f(1)=0,f2(1)=f(f1(1))=f(0)= ![]() ,f3(1)=f(f2(1))=f(
,f3(1)=f(f2(1))=f( ![]() )=1,
)=1,
故①1是f(x)的一个3~周期点,正确;
f1( ![]() )=f(
)=f( ![]() )=1,f2(
)=1,f2( ![]() )=f(f1(
)=f(f1( ![]() ))=f(1)=0,f3(
))=f(1)=0,f3( ![]() )=f(f2(
)=f(f2( ![]() ))=f(0)=
))=f(0)= ![]() ,
,
故②3是点 ![]() 的最小正周期,正确;
的最小正周期,正确;
由已知中的图象可得:f( ![]() )=
)= ![]() ,故f1(
,故f1( ![]() )=f(
)=f( ![]() )=
)= ![]() ,f2(
,f2( ![]() )=f(f1(
)=f(f1( ![]() ))=f(
))=f( ![]() )=
)= ![]() ,f3(
,f3( ![]() )=f(f2(
)=f(f2( ![]() ))=f(
))=f( ![]() )=
)= ![]() ,…
,…
故③对于任意正整数n,都有fn( ![]() )=
)= ![]() ,正确;④若x0=1,则x0∈(
,正确;④若x0=1,则x0∈( ![]() ,1],但x0是f(x)的一个3~周期点,故错误.
,1],但x0是f(x)的一个3~周期点,故错误.
所以答案是:①②③
【考点精析】本题主要考查了函数的图象和命题的真假判断与应用的相关知识点,需要掌握函数的图像是由直角坐标系中的一系列点组成;图像上每一点坐标(x,y)代表了函数的一对对应值,他的横坐标x表示自变量的某个值,纵坐标y表示与它对应的函数值;两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的前n项和为Sn , S3=﹣15,且a1+1,a2+1,a4+1成等比数列,公比不为1.
(1)求数列{an}的通项公式;
(2)设bn= ![]() ,求数列{bn}的前n项和Tn .
,求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在空间四边形ABCD中,E,F,G分别是AB,BC,CD的中点, 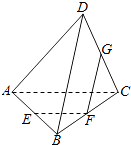
(1)求证:BD∥平面EFG;
(2)若AD=CD,AB=CB,求证:AC⊥BD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中, ![]() =
= ![]() +
+ ![]()
(Ⅰ)求△ABM与△ABC的面积之比
(Ⅱ)若N为AB中点, ![]() 与
与 ![]() 交于点P且
交于点P且 ![]() =x
=x ![]() +y
+y ![]() (x,y∈R),求x+y的值.
(x,y∈R),求x+y的值.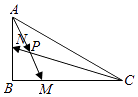
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() ,对于
,对于 ![]() 上的任意x1 , x2 , 有如下条件:
上的任意x1 , x2 , 有如下条件:
① ![]() ;②|x1|>x2;③x1>|x2|;④
;②|x1|>x2;③x1>|x2|;④ ![]() .
.
其中能使g(x1)>g(x2)恒成立的条件序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班主任对全班50名学生学习积极性和对待班级工作的态度进行了调查,统计数据如下表所示:
积极参加班级工作 | 不太主动参加班级工作 | 合计 | |
学习积极性高 | 18 | 7 | 25 |
学习积极性一般 | 6 | 19 | 25 |
合计 | 24 | 26 | 50 |
(1)如果随机抽查这个班的一名学生,那么抽到积极参加班级工作的学生的概率是多少?抽到不太主动参加班级工作且学习积极性一般的学生的概率是多少?
(2)试运用独立性检验的思想方法点拨:学生的学习积极性与对待班级工作的态度是否有关系?并说明理由.(参考下表)
p(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.789 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com