
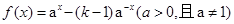 是定义域为
是定义域为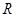 的奇函数.
的奇函数.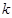 的值;
的值;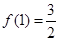 ,且
,且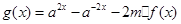 在
在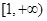 上的最小值为
上的最小值为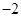 ,求
,求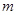 的值.
的值.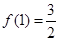 ,试讨论函数
,试讨论函数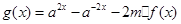 在
在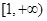 上零点的个数情况。
上零点的个数情况。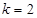 ;(2)
;(2)  (3) 当
(3) 当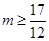 时
时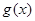 在
在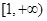 上有一个零点;当
上有一个零点;当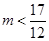 时
时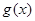 在
在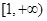 上无零点.
上无零点.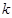 ,可用特殊值或用恒等式对应项系数相等,如果0在奇函数的定义域内,则一定有
,可用特殊值或用恒等式对应项系数相等,如果0在奇函数的定义域内,则一定有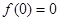 ,如果不在可任取定义域内两个相反数代入求
,如果不在可任取定义域内两个相反数代入求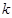 .
.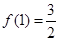 求出
求出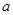 ,代入得
,代入得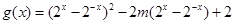 ,换元
,换元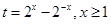 ,注意自变量的取值范围,每设出一个子母都要把它取的范围缩到最小以有利于解题, 所以得到
,注意自变量的取值范围,每设出一个子母都要把它取的范围缩到最小以有利于解题, 所以得到 得到一个新的函数
得到一个新的函数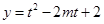 ,
, 利用二次函数函数单调性求最值方法得到
利用二次函数函数单调性求最值方法得到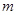 ,二次函数在区间上的最值在端点处或顶点处,遇到对称轴或区间含有待定的字母,则要按对称轴在不在区间内以及区间中点进行讨论.
,二次函数在区间上的最值在端点处或顶点处,遇到对称轴或区间含有待定的字母,则要按对称轴在不在区间内以及区间中点进行讨论.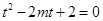 在
在 解个数情况,这个解起来比较麻烦,所以可以用函数单调性先来判定零点的个数,即
解个数情况,这个解起来比较麻烦,所以可以用函数单调性先来判定零点的个数,即 在
在 上为增函数,也就是在
上为增函数,也就是在 这个区间上是一一映射,
这个区间上是一一映射, 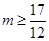 时的每个值方程
时的每个值方程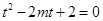 只有一个解.
只有一个解.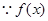 为
为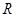 上的奇函数
上的奇函数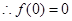 即
即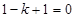
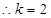
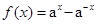
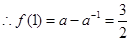 解得
解得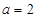 或
或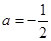 (舍)
(舍) 且
且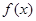 在
在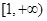 上递增
上递增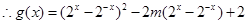
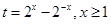 则
则
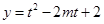 ,
, 且
且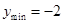
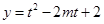 的对称轴为
的对称轴为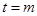
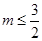 时
时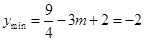
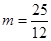 (舍)
(舍)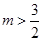 时
时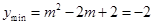


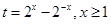 则
则
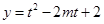 ,
, 零点个数情况
零点个数情况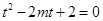 在
在 解个数情况
解个数情况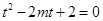 得
得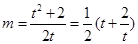 ,
,
 在
在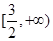 上为增函数
上为增函数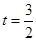 时
时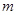 有最小值为
有最小值为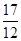
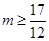 时
时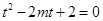 方程在
方程在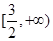 上有一根,即函数有一个零点
上有一根,即函数有一个零点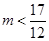 时
时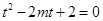 方程在
方程在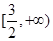 上无根,即函数无零点
上无根,即函数无零点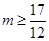 时
时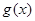 在
在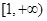 上有一个零点
上有一个零点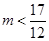 时
时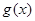 在
在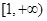 上无零点.
上无零点.

 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com