
【题目】设函数![]()
(Ⅰ)当![]() (
(![]() 为自然对数的底数)时,求
为自然对数的底数)时,求![]() 的极小值;
的极小值;
(Ⅱ)若函数![]() 存在唯一零点,求
存在唯一零点,求![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)![]() 的极小值为2;(Ⅱ)当
的极小值为2;(Ⅱ)当![]() 或
或![]() 时,函数
时,函数![]() 有且只有一个零点.
有且只有一个零点.
【解析】试题分析:(1)先求导数,再求导函数零点,列表分析导函数符号变化规律,进而确定极值(2)先化简![]() ,再利用参变分离法得
,再利用参变分离法得![]() ,利用导数研究函数
,利用导数研究函数![]() ,由图像可得存在唯一零点时
,由图像可得存在唯一零点时![]() 的取值范围
的取值范围
试题解析:(1)由题设,当![]() 时,
时, ![]() ,
,
则![]() ,由
,由![]() ,得
,得![]() .
.
∴当![]() ,
, ![]() ,
, ![]() 在
在![]() 上单调递减,
上单调递减,
当![]() ,
, ![]() ,
, ![]() 在
在![]() 上单调递增,
上单调递增,
∴当![]() 时,
时, ![]() 取得极小值
取得极小值![]() ,
,
∴![]() 的极小值为2.
的极小值为2.
(2)由题设![]() ,
,
令![]() ,得
,得![]() .
.
设![]() ,则
,则![]() ,
,
当![]() 时,
时, ![]() ,
, ![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,
时, ![]() ,
, ![]() 在
在![]() 上单调递减.
上单调递减.
∴![]() 是
是![]() 的唯一极值点,且是极大值点,因此
的唯一极值点,且是极大值点,因此![]() 也是
也是![]() 的最大值点.
的最大值点.
∴![]() 的最大值为
的最大值为![]() .
.
又![]() ,结合
,结合![]() 的图象(如图),可知
的图象(如图),可知
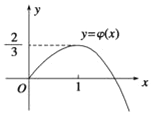
当![]() 时,函数
时,函数![]() 有且只有一个零点;
有且只有一个零点;
当![]() 时,函数
时,函数![]() 有且只有一个零点.
有且只有一个零点.
所以,当![]() 或
或![]() 时,函数
时,函数![]() 有且只有一个零点.
有且只有一个零点.


科目:高中数学 来源: 题型:
【题目】假定下述数据是甲、乙两个供货商的交货天数:
甲:10 9 10 10 11 11 9 11 10 10
乙:8 10 14 7 10 11 10 8 15 12
估计两个供货商的交货情况,并问哪个供货商交货时间短一些,哪个供货商交货时间较具一致性与可靠性.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于定义域为![]() 的函数
的函数![]() ,若满足①
,若满足①![]() ;②当
;②当![]() ,且
,且![]() 时,都有
时,都有![]() ;③当
;③当![]() ,且
,且![]() 时,
时, ![]() ,则称
,则称![]() 为“偏对称函数”.现给出四个函数:
为“偏对称函数”.现给出四个函数:
①![]() ; ②
; ② ![]() ;
;
③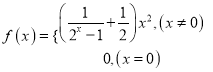 ; ④
; ④![]() .
.
则其中是“偏对称函数”的函数为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AB为圆O的直径,点E、F在圆O上,AB ∥EF,矩形ABCD所在平面与圆O所在的平面互相垂直.已知AB=2,EF=1.
(1)求证:平面DAF⊥平面CBF;
(2)求直线AB与平面CBF所成角的大小;
(3)求AD的长为何值时,平面DFC与平面FCB所成的锐二面角的大小为60°?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的左,右焦点分别为
的左,右焦点分别为![]() ,且
,且![]() 与短轴的一个端点Q构成一个等腰直角三角形,点P(
与短轴的一个端点Q构成一个等腰直角三角形,点P(![]() )在椭圆
)在椭圆![]() 上,过点
上,过点![]() 作互相垂直且与x轴不重合的两直线AB,CD分别交椭圆
作互相垂直且与x轴不重合的两直线AB,CD分别交椭圆![]() 于A,B,C,D且M,N分别是弦AB,CD的中点
于A,B,C,D且M,N分别是弦AB,CD的中点
(1)求椭圆的方程
(2)求证:直线MN过定点R(![]() )
)
(3)求![]() 面积的最大值
面积的最大值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com